
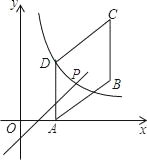
【题目】如图,四边形ABCD是平行四边形,点A(2,0),B(6,2),C(6,6),反比例函数y1=![]() (x>0)的图象过点D,点P是一次函数y2=kx+3﹣3k(k≠0)的图象与该反比例函数的一个公共点,对于下面四个结论:
(x>0)的图象过点D,点P是一次函数y2=kx+3﹣3k(k≠0)的图象与该反比例函数的一个公共点,对于下面四个结论:
①反比例函数的解析式是y1=![]() ;
;
②一次函数y2=kx+3﹣3k(k≠0)的图象一定经过(6,6)点;
③若一次函数y2=kx+3﹣3k的图象经过点C,当x>2![]() 时,y1<y2;
时,y1<y2;
④对于一次函数y2=kx+3﹣3k(k≠0),当y随x的增大而增大时,点P横坐标a的取值范围是0<a<3.
其中正确的是( )
A. ①③ B. ②③ C. ②④ D. ③④
【答案】D
【解析】分析:①根据平行四边形的性质求D点的坐标;(2)把x=6代入y2=kx+3﹣3k中,看函数值是否为6;③把点C的坐标代入y2=kx+3﹣3k,求得一次函数的解析,由一次函数的解析式和反比例函数的解析组成的方程组可求得它们的交点坐标,结合函数图象判断;④一次函数过定点(3,3),确定x=3时的函数值即可.
详解:①∵四边形ABCD是平行四边形,∴AD=BC,
∵B(6,2),C(6,6),∴BC⊥x轴,AD=BC=4,而A点坐标为(2,0),
∴点D的坐标为(2,4),
∵反比例函数y1=![]() (x>0)的函数图象经过点D(2,4),
(x>0)的函数图象经过点D(2,4),
∴4=![]() ,∴m=8,
,∴m=8,
∴反比例函数的解析式为y=![]() ,①不正确;
,①不正确;
②当x=6时,y=kx+3﹣3k=6k+3﹣3k=3k+3≠6,
∴一次函数y=kx+3﹣3k(k≠0)的图象不一定过点C,②不正确;
③∵一次函数y2=kx+3﹣3k的图象经过点C,
∴6=6k+3﹣3k,解得:k=1.
∴y2=x.
联立![]() ,解得:
,解得:![]() 或
或![]() (舍去).
(舍去).
结合函数图象即可得出:
当x>![]() 时,y1<y2,③成立;
时,y1<y2,③成立;
④∵一次函数y2=kx+3﹣3k(k≠0),y随x的增大而增大,
∴k>0,∴交点P在第一象限.
将x=3代入到反比例函数y=![]() 中,得:y=
中,得:y=![]() .
.
∵因为y2-3=k(x﹣3),当x=3时,y2=3,
∴一次函数y2=kx+3﹣3k(k≠0)恒过点(3,3),点(3,![]() )在(3,3)的下方,
)在(3,3)的下方,
即点P应该在点(3,![]() )的左方,∴点P横坐标a的取值范围是a<3.
)的左方,∴点P横坐标a的取值范围是a<3.
即④正确.
综上可知:③④正确,
故选D.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
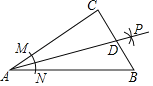
【题目】如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D.若AC=9,AB=15,且S△ABC=54,则△ABD的面积是( )
MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D.若AC=9,AB=15,且S△ABC=54,则△ABD的面积是( )
A. ![]() B.
B. ![]() C. 45D. 35
C. 45D. 35
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:

①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是 .(把你认为正确说法的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
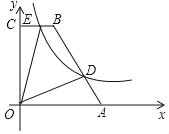
【题目】如图,在四边形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0),(2,6),点D为AB上一点,且![]() ,双曲线y=
,双曲线y=![]() (k>0)经过点D,交BC于点E
(k>0)经过点D,交BC于点E
(1)求双曲线的解析式;
(2)求四边形ODBE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试,他们各自的成绩(百分制)如下表:
选手 | 表达能力 | 阅读理解 | 综合素质 | 汉字听写 |
甲 | 85 | 78 | 85 | 73 |
乙 | 73 | 80 | 82 | 83 |
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁;
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们20%、10%、30%和40%的权重,请分别计算两名选手的最终成绩,从他们的这一成绩看,应选派谁.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地图书馆为了满足群众多样化阅读的需求,决定购买甲、乙两种品牌的电脑若干组建电子阅览室.经了解,甲、乙两种品牌的电脑单价分别3100元和4600元.
(1)若购买甲、乙两种品牌的电脑共50台,恰好支出200000元,求甲、乙两种品牌的电脑各购买了多少台?
(2)若购买甲、乙两种品牌的电脑共50台,每种品牌至少购买一台,且支出不超过160000元,共有几种购买方案?并说明哪种方案最省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,给出五个等量关系:①AD=BC;②AC=BD;③CE=DE;④∠D=∠C;⑤∠DAB=∠CBA.
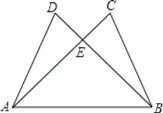
请你以其中两个为条件,另外三个中的一个为结论,推出一个正确的结论(只需写出一种情况),并加以证明.
已知:
求证:
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,AB′与CD交于点E.
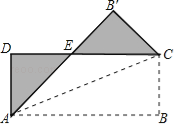
(1)求证:△AED≌△CEB′;
(2)求证:点E在线段AC的垂直平分线上;
(3)若AB=8,AD=3,求图中阴影部分的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高服务质量,某宾馆决定对甲、乙两种套房进行星级提升,已知甲种套房提升费用比乙种套房提升费用少3万元,如果提升相同数量的套房,甲种套房费用为625万元,乙种套房费用为700万元.
(1)甲、乙两种套房每套提升费用各多少万元?
(2)如果需要甲、乙两种套房共80套,市政府筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于甲、乙种套房星级提升,市政府对两种套房的提升有几种方案?哪一种方案的提升费用最少?
(3)在(2)的条件下,根据市场调查,每套乙种套房的提升费用不会改变,每套甲种套房提升费用将会提高a万元(a>0),市政府如何确定方案才能使费用最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com