
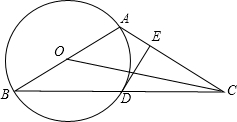
 如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点D恰好为BC的中点.过点D作DE⊥AC交AC边于点E.
如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点D恰好为BC的中点.过点D作DE⊥AC交AC边于点E.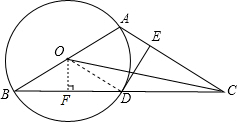 (1)证明:连接OD.
(1)证明:连接OD.| 1 |
| 2 |
| ||
| 2 |
3
| ||
| 2 |
| FO |
| FC |
| ||||
|
| 1 | ||
3
|
| ||
| 9 |
| 1 |
| 2 |
| ||
| 2 |
3
| ||
| 2 |


科目:初中数学 来源: 题型:
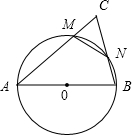 如图,以△ABC的边AB为直径画圆,与边AC交于M,与边BC交于N,已知△ABC的面积是△CMN面积的4倍,△ABC中有一个内角度数是另一内角度数的2倍,试计算△ABC三个内角的度数:
如图,以△ABC的边AB为直径画圆,与边AC交于M,与边BC交于N,已知△ABC的面积是△CMN面积的4倍,△ABC中有一个内角度数是另一内角度数的2倍,试计算△ABC三个内角的度数:查看答案和解析>>
科目:初中数学 来源: 题型:
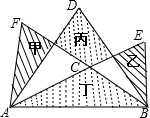 如图,以△ABC的每一条边为边作三个正三角形△ABD、△BCE和△ACF.已知这三个正三角形构成的图形中,甲、乙阴影部分的面积和等于丙、丁阴影部分的面积和,则∠FCE=( )
如图,以△ABC的每一条边为边作三个正三角形△ABD、△BCE和△ACF.已知这三个正三角形构成的图形中,甲、乙阴影部分的面积和等于丙、丁阴影部分的面积和,则∠FCE=( )| A、130° | B、140° | C、150° | D、160° |
查看答案和解析>>
科目:初中数学 来源: 题型:
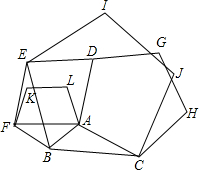 (2012•拱墅区一模)如图,以△ABC的各边为边,在BC的同侧分别作三个正五边形.它们分别是正五边形ABFKL、BCJIE、ACHGD,试探究:
(2012•拱墅区一模)如图,以△ABC的各边为边,在BC的同侧分别作三个正五边形.它们分别是正五边形ABFKL、BCJIE、ACHGD,试探究:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com