【题目】把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G、D、C分别在M、N的位置上，若∠EFG=55°，则∠1=_°，∠2=°．
【答案】70°；110°
【解析】解：∵一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G，D，C分别在M，N的位置上，
∴∠GEF=∠FED，
∵AD∥BC，∠EFG=55°，
∴∠FED=∠EFG=55°，
∵∠1+∠GEF+∠FED=180°，
∴∠1=180°﹣55°﹣55°=70°，
∵AD∥BC
∴∠1+∠2=180°，
∴∠2=180°﹣70°=110°．
故答案为：70°，110°．
根据折叠的性质得出∠GEF=∠FED，根据二直线平行内错角相等得出∠FED=∠EFG=55°，根据平角的定义得出∠1+∠GEF+∠FED=180°，从而得出∠1的度数，然后再根据二直线平行，同旁内角互补得出∠2的度数。
科目：初中数学 来源： 题型：
【题目】自开展“学生每天锻炼1小时”活动后，我市某中学根据学校实际情况，决定开设A：毽子，B：篮球，C：跑步，D：跳绳四种运动项目．为了了解学生最喜欢哪一种项目，随机抽取了部分学生进行调查，并将调查结果绘制成如图统计图．请结合图中信息解答下列问题：
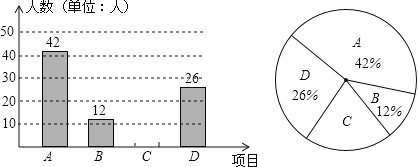
（1）该校本次调查中，共调查了多少名学生？
（2）请将两个统计图补充完整；
（3）在本次调查的学生中随机抽取1人，他喜欢“跑步”的概率有多大？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读理解：小明热爱数学，在课外书上看到了一个有趣的定理——“中线长定理”：三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍．如图1，在△ABC中，点D为BC的中点，根据“中线长定理”，可得：
AB2＋AC2＝2AD2＋2BD2．
小明尝试对它进行证明，部分过程如下：
解：过点A作AE⊥BC于点E，如图2，在Rt△ABE中，AB2＝AE2＋BE2，
同理可得：AC2＝AE2＋CE2，AD2＝AE2＋DE2，
为证明的方便，不妨设BD＝CD＝x，DE＝y，
∴AB2＋AC2＝AE2＋BE2＋AE2＋CE2＝……
（1）请你完成小明剩余的证明过程；
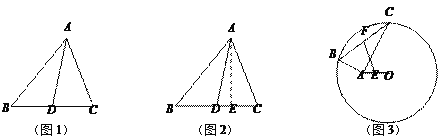
理解运用：
（2） ① 在△ABC中，点D为BC的中点，AB＝6，AC＝4，BC＝8，则AD＝_______；
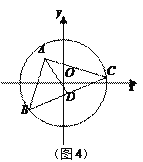
② 如图3，⊙O的半径为6，点A在圆内，且OA＝2
，点B和点C在⊙O上，且∠BAC＝90°，点E、F分别为AO、BC的中点，则EF的长为________；
拓展延伸：
（3）小明解决上述问题后，联想到《能力训练》上的题目：如图4，已知⊙O的半径为5
，以A(3，4)为直角顶点的△ABC的另两个顶点B，C都在⊙O上，D为BC的中点，求AD长的最大值．请你利用上面的方法和结论，求出AD长的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】今年要实现大病保险全覆盖，中央财政安排城乡医疗救助补助资金160亿元，160亿元这一数据用科学记数法表示为（ ）
A.16×109元
B.1.6×1010元
C.0.16×1011元
D.1.6×109元
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD，如图1，再在矩形纸板的四个角上切去边长相等的小正方形，再把它的边沿虚线折起，做成一个无盖的长方体纸盒，底面为矩形EFGH，如图2．设小正方形的边长为x厘米．
（1）当矩形纸板ABCD的一边长为90厘米时，求纸盒的侧面积的最大值；
（2）当EH：EF＝7：2，且侧面积与底面积之比为9：7时，求x的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了响应“足球进校园”的目标，某校计划为学校足球队购买一批足球，已知购买2个A品牌的足球和3个B品牌的足球共需380元；购买4个A品牌的足球和2个B品牌的足球共需360元．
（1）求A，B两种品牌的足球的单价．
（2）求该校购买20个A品牌的足球和2个B品牌的足球的总费用．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，A（1，2），B（3，1），C（﹣2，﹣1）．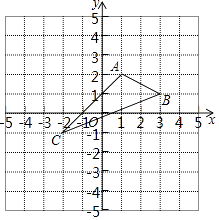 
（1）在图中作出△ABC关于x轴的对称图形△A1B1C1 ．
（2）写出点A1 ， B1 ， C1的坐标（直接写答案）
A1
B1
C1
（3）求△ABC的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com