
分析 ①利用因式分解法解方程;
②利用直接开平方法解方程.
解答 解:①[3x-1+3(3x+1)][3x-1-3(3x+1)]=0,
3x-1+3(3x+1)=0或3x-1-3(3x+1)=0,
所以x1=-$\frac{1}{6}$,x2=$\frac{2}{3}$;
②2x-$\sqrt{3}$+$\sqrt{2}$=0
所以x1=x2=$\frac{\sqrt{3}-\sqrt{2}}{2}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了直接开平方法解一元二次方程.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
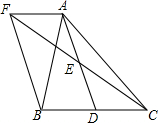 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,线段AB的长为l.
如图,线段AB的长为l.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
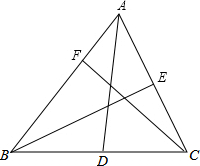 如图,在△ABC中,
如图,在△ABC中,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com