Question

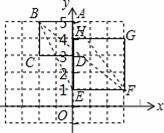
如图，正方形ABCD与正方形EFGH是位似形，已知A（0，5），D（0，3），E（0，1），H（0，4），则位似中心的坐标是　　　　　　．

　

Answer 1

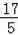
（0，），（﹣6，13）　．

【考点】位似变换；坐标与图形性质．

【分析】分别利用待定系数法求出一次函数解析式，再利用当B与F是对应点，以及当B与E是对应点分别求出位似中心．

【解答】解：设当B与F是对应点，设直线BF的解析式为：y=kx+b，

则，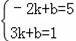

解得：，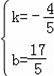

故直线BF的解析式为：y=﹣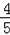x+，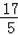

则x=0时，y=，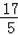

即位似中心是：（0，），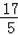

设当B与E是对应点，设直线BE的解析式为：y=ax+c，

则，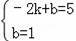

解得：，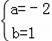

故直线BE的解析式为：y=﹣2x+1，

设直线HF的解析式为：y=dx+e，

则，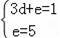

解得：，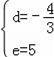

故直线HF的解析式为：y=﹣x+5，

则，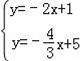

解得：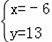

即位似中心是：（﹣6，13），

综上所述：所述位似中心为：（0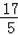，），（﹣6，13）．

故答案为：（0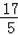，），（﹣6，13）．

【点评】此题主要考查了位似图形的性质以及待定系数法求一次函数解析式，正确分类讨论得出是解题关键．