
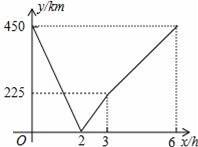
һ�п쳵�ɼؿ����ҵأ�һ���������ҵؿ����أ�����ͬʱ�����������˶����쳵���ҵصľ���y1��km������ʻ��ʱ��x��h��֮��ĺ�����ϵ��ͼ1���߶�AB��ʾ���������ҵصľ���y2��km������ʻ��ʱ��x ��h��֮��ĺ�����ϵ��ͼ1���߶�OC��ʾ������ͼ����������о���


��1���ֱ����߶�AB��OC��Ӧ�ĺ�������ʽy1��y2��
��2����졢����֮��ľ���ΪS����S��km����������ʻʱ��x��h���ĺ�����ϵʽ��������������ͼ��
��3����졢����֮��ľ��볬��135kmʱ��x��ȡֵ��Χ��
�����㡿һ�κ�����Ӧ�ã�
����������1�����õ�A����Ϊ��0��450�������Եó��ף�������֮��ľ���Ϊ450�����õ�A����Ϊ��0��450������B����Ϊ��3��0��������y1=kx+b������ɣ������߶�OC����ʽΪy=ax������ɣ�
��2�����ã�1��������ó�S=|y1��y2|�����������������ʽ���ó�ͼ�ɣ�
��3��S=135ʱ���������������225x+450=135��225x��450=135����ã�x=1.4��x=2.6��졢����֮��ľ��볬��135kmʱ��x��ȡֵ��Χ��0��x��1.4��2.6��x��6��
����𡿽⣺��1�����߶�AB�ĺ�������ʽΪy1=kx+b��
�ѵ�A����Ϊ��0��450������B����Ϊ��3��0��������y1=kx+b�ã�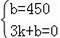

��ã�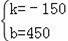

��y1=��150x+450��
���߶�OC�ĺ�������ʽΪy=ax��
�ѣ�6��450������y=ax�ã�6a=450��
��ã�a=75��
��y2=75x��
��2�����ݣ�1���ó���
S=|y1��y2|=|450��150x����75x|=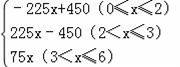

����ͼ����ͼ��ʾ��

��3��S=135ʱ�������������
��225x+450=135��225x��450=135��
��ã�x=1.4��x=2.6
��졢����֮��ľ��볬��135kmʱ��x��ȡֵ��Χ��0��x��1.4��2.6��x��6��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͬһʱ�̵�������,С����Ӱ�ӱ�Сǿ��Ӱ�ӳ�,��ô��ͬһ·���� ( )
(A)С����Ӱ�ӱ�Сǿ��Ӱ�ӳ�. (B)С����Ӱ�ӱ�Сǿ��Ӱ�Ӷ�.
(C)С����Ӱ�Ӻ�Сǿ��Ӱ��һ����. (D)���ж�˭��Ӱ�ӳ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
���� �������ֵ��(����)��
�������ֵ��(����)��
A��(��5)3��2 B����(53��2)
C����53��2 D��53��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
.����������һ���ϵĸ���Ϊ1���Ҹ�����ױߵļнǵ�����ֵΪ1����������������ε����Ϊ�� ����
A  B 1 C
B 1 C  D
D 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�������������У���ABC��λ����ͼ��ʾ����
 ��ֵΪ�� ����
��ֵΪ�� ����
A��1 B�� C��
C��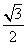 D��
D��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����ͼ����·������CF��DE����ƽ�У��߶�CDΪ���к������·�����A��B����ֱ��ʾ��վ�ͳ��У�CD��AB����ֱ����ƽ�У��Ҷ�����·�����ߴ�ֱ����·��20�ף�A��B���62�ף���A=67�㣬��B=37�㣮
��1����CD��AB֮��ľ��룻
��2��ij�˴ӳ�վA������������A��D��C��Bȥ����B������������A��D��C��B���ﳬ�б�ֱ�Ӻᴩ��·���߶����ף�
���ο����ݣ�sin67���
 ��cos67���
��cos67���
 ��tan67���
��tan67���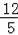
 ��sin37���
��sin37���
 ��cos37���
��cos37���
 ��tan37���
��tan37���
 ��
��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��������ABCD��������EFGH��λ���Σ���֪A��0��5����D��0��3����E��0��1����H��0��4������λ�����ĵ���������������������


��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����ͼ���м�����Գ�ͼ���������ĶԳ�ͼ�ε��ǣ� ��
��A��������� ��B���������� ��C������������ ��D����������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com