
ЁОЬтФПЁПФГбјжГЙЋЫОзМБИдЫЫЭ152ЯфаЁСњЯКЕНAЁЂBСНЕиЯњЪлЃЌИУХњаЁСњЯКИеКУФмгУДѓаЁЛѕГЕ15СОвЛДЮдЫЭъЃЌвбжЊДѓЛѕГЕУПСОФмзА12ЯфЃЌаЁЛѕГЕУПСОФмзА8ЯфЃЌЦфжаУПСОДѓЛѕГЕдЫЭљAЁЂBСНЕиЕФдЫЗбЗжБ№ЮЊ800дЊКЭ900дЊЃЛУПСОаЁЛѕГЕдЫЭљAЁЂBСНЕиЕФдЫЗбЗжБ№ЮЊ400дЊКЭ600дЊЃЎ
ЃЈ1ЃЉЧѓет15СОГЕжаДѓаЁЛѕГЕИїгаЖрЩйСОЃП
ЃЈ2ЃЉЯжАВХХЦфжа10СОЛѕГЕЧАЭљAЕиЃЌЦфгрЛѕГЕЧАЭљBЕиЃЌЩшЧАЭљAЕиЕФДѓЛѕГЕЮЊmСОЃЌЧАЭљAЁЂBСНЕизмЗбгУЮЊyдЊЃЌЪдЧѓГіyгыmЕФКЏЪ§НтЮіЪНЃЌВЂаДГіmЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШєдЫЭљBЕиЕФЗбгУВЛИпгкAЕиЗбгУЕФвЛАыЃЌЧѓДЫЪБЕФзюЕЭзмдЫЗбЃЎ
ЁОД№АИЁПЃЈ1ЃЉДѓЛѕГЕ8СОЃЌаЁЛѕГЕ7СОЃЛЃЈ2ЃЉy=100x+9400ЃЎЃЈ3ЁмxЁм8ЃЉЃЛЃЈ3ЃЉДЫЪБЕФзюЕЭзмдЫЗбЪЧ10100дЊЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЩшДѓЛѕГЕгУxСОЃЌаЁЛѕГЕгУyСОЃЌИљОнДѓЁЂаЁСНжжЛѕГЕЙВ15СОЃЌдЫЪф152ЯфаЁСњЯКЃЌСаЗНГЬзщЧѓНтЃЛ
ЃЈ2ЃЉЩшЧАЭљAЕиЕФДѓЛѕГЕЮЊxСОЃЌдђЧАЭљBЕиЕФДѓЛѕГЕЮЊЃЈ8-xЃЉСОЃЌЧАЭљAЕиЕФаЁЛѕГЕЮЊЃЈ10-xЃЉСОЃЌЧАЭљBЕиЕФаЁЛѕГЕЮЊ[7-ЃЈ10-xЃЉ]СОЃЌИљОнБэИёЫљИјдЫЗбЃЌЧѓГіyгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉНсКЯвбжЊЬѕМўЃЌЧѓxЕФШЁжЕЗЖЮЇЃЌгЩЃЈ2ЃЉЕФКЏЪ§ЙиЯЕЪННсКЯвЛДЮКЏЪ§ЕФаджЪЧѓЪЙзмдЫЗбзюЩйЕФЛѕГЕЕїХфЗНАИЃЎ
ЃЈ1ЃЉЩшДѓЛѕГЕxСОЃЌаЁЛѕГЕyСО
вРЬтвтЃЌЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁрДѓЛѕГЕ8СОЃЌаЁЛѕГЕ7СОЃЛ
ЃЈ2ЃЉЁпЧАЭљAЕиЕФДѓЛѕГЕЮЊxСОЃЌЙВга10СОЛѕГЕЧАЭљAЕиЃЎ
ЁрЧАЭљAЕиЕФаЁЛѕГЕЮЊЃЈ10ЉxЃЉЃЌЧАЭљBЕиЕФДѓЛѕГЕЮЊЃЈ8ЉxЃЉСОЃЌ
аЁЛѕГЕЮЊ[7ЉЃЈ10ЉxЃЉЃНxЉ3]СО
yЃН800x+400ЃЈ10ЉxЃЉ+900ЃЈ8ЉxЃЉ+600ЃЈxЉ3ЃЉ
ЃН800x+4000Љ400x+7200Љ900xЉ1800+600x
ЃН100x+9400ЃЎЃЈ3ЁмxЁм8ЃЉЃЛ
ЃЈ3ЃЉвРЬтвтЃЌЕУ900ЃЈ8ЉxЃЉ+600ЃЈxЉ3ЃЉЁм![]() [800x+400ЃЈ10ЉxЃЉ]
[800x+400ЃЈ10ЉxЃЉ]
ећРэЕУ500xЁн3400
ЁрxЁн![]()
Ёп0ЁмxЁм8ЃЌЧвxЪЧећЪ§
ЁрxЃН7Лђ8ЃЌ
Ёп100ЃО0ЃЌ
ЁрyЃН100x+9400ЪЧдіКЏЪ§ЃЎ
ЁрЕБxЃН7ЪБЃЌyзюаЁЃН100ЁС7+9400ЃН10100
ЁрДЫЪБЕФзюЕЭзмдЫЗбЪЧ10100дЊЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
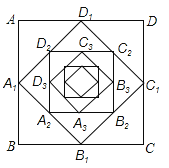
ЁОЬтФПЁПСЌНге§ЗНаЮЫФБпЕФжаЕуЫљЙЙГЩЕФе§ЗНаЮЃЌЮвУЧГЦЦфде§ЗНаЮЕФжаЕуе§ЗНаЮЃЌШчЭМЃЌвбжЊе§ЗНаЮ![]() ЕФжаЕуе§ЗНаЮ
ЕФжаЕуе§ЗНаЮ![]() ЃЌдйзїе§ЗНаЮ
ЃЌдйзїе§ЗНаЮ![]() ЕФжаЕуе§ЗНаЮ
ЕФжаЕуе§ЗНаЮ![]() ЃЌетбљВЛЖЯЯТШЅЃЌЕкnДЮЫљзіЕФжаЕуе§ЗНаЮ
ЃЌетбљВЛЖЯЯТШЅЃЌЕкnДЮЫљзіЕФжаЕуе§ЗНаЮ![]() ЃЌШєе§ЗНаЮ
ЃЌШєе§ЗНаЮ![]() ЕФБпГЄЮЊ1ЃЌШєЩшжаЕуе§ЗНаЮ
ЕФБпГЄЮЊ1ЃЌШєЩшжаЕуе§ЗНаЮ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌдђ
ЃЌдђ![]() ___________ЃЎ
___________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() жсе§АыжсЩЯвЛЖЏЕуЃЌСЌНг
жсе§АыжсЩЯвЛЖЏЕуЃЌСЌНг![]() ЃЌНЋ
ЃЌНЋ![]() би
би![]() ЗелЕУ
ЗелЕУ![]() ЃЌЕу
ЃЌЕу![]() ЗжБ№ЮЊ
ЗжБ№ЮЊ![]() ЕФжаЕуЃЌСЌНг
ЕФжаЕуЃЌСЌНг![]() ВЂбгГЄНЛ
ВЂбгГЄНЛ![]() ЫљдкжБЯпгкЕу
ЫљдкжБЯпгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎЕБ
ЃЎЕБ![]() ЮЊжБНЧШ§НЧаЮЪБЃЌЕу
ЮЊжБНЧШ§НЧаЮЪБЃЌЕу![]() зјБъЮЊ_______ЃЎ
зјБъЮЊ_______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
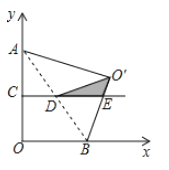
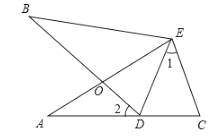
ЁОЬтФПЁПЕуAЪЧКЏЪ§yЃН![]() ЃЈxЃО0ЃЉЩЯвЛЖЏЕуЃЌСЌНгOAЃЌЯпЖЮOBгыOAЙигкyжсЖдГЦЃЌНЋЯпЖЮOAШЦЕуOФцЪБеыа§зЊ90ЁуЕУЯпЖЮOCЃЌНЋЯпЖЮOAШЦЕуAФцЪБеыа§зЊ90ЁуЕУЯпЖЮDAЃЎ
ЃЈxЃО0ЃЉЩЯвЛЖЏЕуЃЌСЌНгOAЃЌЯпЖЮOBгыOAЙигкyжсЖдГЦЃЌНЋЯпЖЮOAШЦЕуOФцЪБеыа§зЊ90ЁуЕУЯпЖЮOCЃЌНЋЯпЖЮOAШЦЕуAФцЪБеыа§зЊ90ЁуЕУЯпЖЮDAЃЎ

ЃЈ1ЃЉдкЭМ1жаЛГіЯпЖЮOBЁЂOCЃЌБЃСєзїЭМКлМЃЃЛ
ЃЈ2ЃЉСЌНгABЁЂBCЁЂACЃЌЕБЁїAOBЕФУцЛ§ЕШгкЁїBOCЕФУцЛ§ЪБЃЌЧѓЁїABCЕФУцЛ§ЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌШєЕуDЕФзјБъЮЊЃЈmЃЌnЃЉЃЌжБНгаДГіmгыnЕФЕШСПЙиЯЕЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
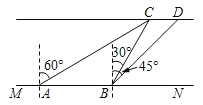
ЁОЬтФПЁПаЁУїЯывЊВтСПЫЎУцШЫЙЄЕКЩЯСНПУаЁЪїCDЕФОрРыЃЌШчЭМЃЌвбжЊКгАЖMNЁЮCDЃЌаЁУїдкКгАЖMNЩЯЕуAДІВтСПаЁЪїCЮЛгкББЦЋЖЋ60ЁуЗНЯђЃЌШЛКѓбиКгАЖзпСЫ20УзЃЌЕНДяЕуBДІЃЌДЫЪБВтЕУКгЖдАЖаЁЪїCЮЛгкББЦЋЖЋ30ЁуЗНЯђЃЌаЁЪїDЮЛгкЖЋББЗНЯђЃЌдђСНПУЪїCDЕФОрРыЮЊ_____УзЃЎЃЈНсЙћБЃСєИљКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
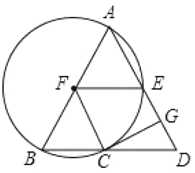
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌвд
ЃЌвд![]() ЮЊжБОЖЕФ
ЮЊжБОЖЕФ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЬюПеЃКЂйШє![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЕФУцЛ§ЮЊ ЁЁЁЁЁЁ ЃЛ
ЕФУцЛ§ЮЊ ЁЁЁЁЁЁ ЃЛ
ЂкЕБ![]() ЕФЖШЪ§ЮЊ ЁЁЁЁЁЁ ЪБЃЌЫФБпаЮ
ЕФЖШЪ§ЮЊ ЁЁЁЁЁЁ ЪБЃЌЫФБпаЮ![]() ЪЧСтаЮЃЎ
ЪЧСтаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁАДДШЋЙњЮФУїГЧЪаЁБЛюЖЏжаЃЌФГЩчЧјЮЊСЫСЫНтОгУёеЦЮеРЌЛјЗжРржЊЪЖЕФЧщПіНјааЕїВщЃЎЦфжаAЁЂBСНаЁЧјЗжБ№га500УћОгУёЃЌЩчЧјДгжаИїЫцЛњГщШЁ50УћОгУёНјааЯрЙижЊЪЖВтЪдЃЌВЂНЋГЩМЈНјааећРэЕУЕНВПЗжаХЯЂЃК
ЃЈаХЯЂвЛЃЉAаЁЧј50УћОгУёГЩМЈЕФЦЕЪ§жБЗНЭМШчЭМЃЈУПвЛзщКЌЧАвЛИіБпНчжЕЃЌВЛКЌКѓвЛИіБпНчжЕЃЉЃЛ
ЃЈаХЯЂЖўЃЉЭМжаЃЌДгзѓЭљгвЕкЫФзщЕФГЩМЈШчЯТ
75 | 75 | 79 | 79 | 79 | 79 | 80 | 80 |
81 | 82 | 82 | 83 | 83 | 84 | 84 | 84 |
ЃЈаХЯЂШ§ЃЉAЁЂBСНаЁЧјИї50УћОгУёГЩМЈЕФЦНОљЪ§ЁЂжаЮЛЪ§ЁЂжкЪ§ЁЂгХауТЪЃЈ80ЗжМАвдЩЯЮЊгХауЃЉЁЂЗНВюЕШЪ§ОнШчЯТЃЈВПЗжПеШБЃЉЃК
аЁЧј | ЦНОљЪ§ | жаЮЛЪ§ | жкЪ§ | гХауТЪ | ЗНВю |
A | 75.1 | 79 | 40% | 277 | |
B | 75.1 | 77 | 76 | 45% | 211 |
ИљОнвдЩЯаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧѓAаЁЧј50УћОгУёГЩМЈЕФжаЮЛЪ§ЃЎ
ЃЈ2ЃЉЧыЙРМЦAаЁЧј500УћОгУёжаФмГЌЙ§ЦНОљЪ§ЕФгаЖрЩйШЫЃП
ЃЈ3ЃЉЧыОЁСПДгЖрИіНЧЖШБШНЯЁЂЗжЮіAЃЌBСНаЁЧјОгУёеЦЮеРЌЛјЗжРржЊЪЖЕФЧщПіЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() БпЩЯЃЌ
БпЩЯЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЃЈ3ЃЉШє![]() ЃЌЕБ
ЃЌЕБ![]() ЕФЭтаФдкжБЯп
ЕФЭтаФдкжБЯп![]() ЩЯЪБЃЌ
ЩЯЪБЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
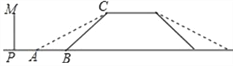
ЁОЬтФПЁПФГЕиЕФвЛзљШЫааЬьЧХШчЭМЫљЪОЃЌЬьЧХИпЮЊ6УзЃЌЦТУцBCЕФЦТЖШЮЊ1ЃК1ЃЌЮЊСЫЗНБуааШЫЭЦГЕЙ§ЬьЧХЃЌгаЙиВПУХОіЖЈНЕЕЭЦТЖШЃЌЪЙаТЦТУцЕФЦТЖШЮЊ1ЃК![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓаТЦТУцЕФЦТНЧЁЯCABЕФЖШЪ§ЃЛ
ЃЈ2ЃЉдЬьЧХЕзВПе§ЧАЗН8УзДІЃЈPBЕФГЄЃЉЕФЮФЛЏЧНPMЪЧЗёашвЊВ№Г§ЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com