
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() 是
是![]() 的切线;
的切线;![]() 交
交![]() 于点
于点![]() .
.
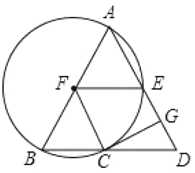
(1)求证:![]() ;
;
(2)填空:①若![]() 的面积为
的面积为![]() ,则
,则![]() 的面积为 ;
的面积为 ;
②当![]() 的度数为 时,四边形
的度数为 时,四边形![]() 是菱形.
是菱形.
【答案】(1)见解析;(2)①60;②当 ![]() 的度数为
的度数为 ![]() 时,四边形
时,四边形 ![]() 是菱形,理由见解析
是菱形,理由见解析
【解析】
(1)可先证明CF∥AD,再根据![]() 是
是![]() 的切线,推出
的切线,推出![]() ,继而得出结论;
,继而得出结论;
(2)①可得出![]() ,得出
,得出![]() ,再根据面积比等于边长比的平方即可得出答案;②当
,再根据面积比等于边长比的平方即可得出答案;②当 ![]() 的度数为
的度数为 ![]() 时,四边形
时,四边形 ![]() 是菱形,先证明四边形是平行四边形,再证其是菱形.
是菱形,先证明四边形是平行四边形,再证其是菱形.
解:(1) ![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
∴CF∥AD,
![]() 是
是 ![]() 的切线,
的切线,
![]() ,
,
![]() .
.
(2) ![]() ;
;![]()
① ∵CF∥AD,
![]() ,
,
![]() ,
,
的面积:
![]() 的面积=
的面积=![]() ,
,
![]() 的面积=
的面积=![]() 的面积=
的面积=![]() ;
;
②当 ![]() 的度数为
的度数为 ![]() 时,四边形
时,四边形 ![]() 是菱形.
是菱形.
理由如下:
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,
![]() ,
,
又 ∵CF∥AD,
![]() 四边形
四边形 ![]() 是平行四边形,
是平行四边形,
![]() ,
,
![]() 平行四边形
平行四边形 ![]() 是菱形.
是菱形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图点![]() 分别是边长为4cm的等边三角形
分别是边长为4cm的等边三角形![]() 边
边![]() 动点,点
动点,点![]() 从顶点
从顶点![]() 沿
沿![]() 向点
向点![]() 运动,点
运动,点![]() 同时从顶点
同时从顶点![]() 沿
沿![]() 向
向![]() 运动,它们的速度都是
运动,它们的速度都是![]() ,当到达终点时停止运动,设运动时间为t秒,连接
,当到达终点时停止运动,设运动时间为t秒,连接![]() 交于点M.
交于点M.
(1)求证:![]() ;
;
(2)点![]() 在运动的过程中,
在运动的过程中,![]() 变化吗?若变化,请说明理由,若不变,则求出它的度数;
变化吗?若变化,请说明理由,若不变,则求出它的度数;
(3)当![]() 为何值时
为何值时![]() 是直角三角形?
是直角三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰![]() 中,
中,![]() ,作
,作![]() 的平分线交
的平分线交![]() 于点
于点![]() ,将
,将![]() 绕点
绕点![]() 旋转,使
旋转,使![]() 的两边交直线
的两边交直线![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)当![]() 绕点
绕点![]() 旋转到如图①的位置时,请直接写出三条线段
旋转到如图①的位置时,请直接写出三条线段![]() 的数量关系;
的数量关系;
(2)当![]() 绕点
绕点![]() 旋转到如图②的位置时,(1)中结论是否成立,若成立,请证明;若不成立,请写出正确的结论,并说明理由;
旋转到如图②的位置时,(1)中结论是否成立,若成立,请证明;若不成立,请写出正确的结论,并说明理由;
(3)若![]() ,当
,当![]() 时,请直接写出线段
时,请直接写出线段![]() 的长度.
的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖公司准备运送152箱小龙虾到A、B两地销售,该批小龙虾刚好能用大小货车15辆一次运完,已知大货车每辆能装12箱,小货车每辆能装8箱,其中每辆大货车运往A、B两地的运费分别为800元和900元;每辆小货车运往A、B两地的运费分别为400元和600元.
(1)求这15辆车中大小货车各有多少辆?
(2)现安排其中10辆货车前往A地,其余货车前往B地,设前往A地的大货车为m辆,前往A、B两地总费用为y元,试求出y与m的函数解析式,并写出m的取值范围;
(3)在(2)的条件下,若运往B地的费用不高于A地费用的一半,求此时的最低总运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受益于国家支持新能源汽车发展和“一带一路”发展战略等多重利好因素,我市某汽车零部件生产企业的利润逐年提高,据统计,2016年利润为3亿元,2018年利润为4.32亿元.
(1)求该企业从2016年到2018年利润的年平均增长率;
(2)若2019年保持前两年利润的年平均增长率不变,该企业2019年的利润能否超过5亿元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个寻宝游戏的寻宝通道如图①所示,通道由在同一平面内的AB,BC,CA,OA, OB,OC组成。为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图像大致如图②所示,则寻宝者的行进路线可能为:
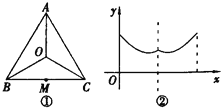
A. A→O→B B. B→A→C C. B→O→C D. C→B→O
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com