
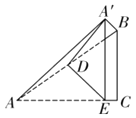
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,将
上,将![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 落在点
落在点![]() 处,连接
处,连接![]() 、
、![]() ,当
,当![]() 是等腰直角三角形时,
是等腰直角三角形时,![]() 的长为________.
的长为________.
【答案】1
【解析】
由![]() ,
,![]() ,
,![]() ,可得∠BAC=30°,又由
,可得∠BAC=30°,又由![]() 是
是![]() 的中点,可得DA=BD=
的中点,可得DA=BD=![]() AB=2,再根据将
AB=2,再根据将![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 落在点
落在点![]() 处,可得
处,可得![]() D=2,则∠BAC=90°, AD=
D=2,则∠BAC=90°, AD=![]() D=2;又
D=2;又![]() 是等腰直角三角形,则∠
是等腰直角三角形,则∠![]() AC=45°,即可求得∠
AC=45°,即可求得∠![]() AB=∠D
AB=∠D![]() A=15°,再由三角形外角的定义可得∠
A=15°,再由三角形外角的定义可得∠![]() DB=30°,最后根据直角三角形中30°多对的边为斜边的一半即可解答.
DB=30°,最后根据直角三角形中30°多对的边为斜边的一半即可解答.
解:∵![]() ,
,![]() ,
,![]()
∴sin∠BAC=![]()
∴∠BAC=30°,
∵![]() 是
是![]() 的中点
的中点
∴DA=BD=![]() AB=2
AB=2
∵将![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 落在点
落在点![]() 处,
处,
∴![]() D=2
D=2
∴DA=BD=![]() D=2
D=2
∴∠BAC=90°, ∠![]() AB=∠D
AB=∠D![]() A
A
又∵![]() 是等腰直角三角形
是等腰直角三角形
∴∠![]() AC=45°
AC=45°
∴∠![]() AB=∠D
AB=∠D![]() A=∠
A=∠![]() AC -∠BAC =15°,
AC -∠BAC =15°,
∴∠![]() DB=∠
DB=∠![]() AB+∠D
AB+∠D![]() A=30°
A=30°
∴![]() =
=![]() =1
=1
故答案为1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】刘徵是我国古代最杰出的数学家之一,他在《九算术圆田术)中用“割圆术”证明了圆面积的精确公式,并给出了计算圆周率的科学方法(注:圆周率=圆的周长与该圆直径的比值)“割圆术”就是以“圆内接正多边形的面积”,来无限逼近“圆面积”,刘徽形容他的“割圆术”说:割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣.刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径R.此时圆内接正六边形的周长为6R,如果将圆内接正六边形的周长等同于圆的周长,可得圆周率为3.当正十二边形内接于圆时,如果按照上述方法计算,可得圆周率为_____.(参考数据:sinl5°=0.26)
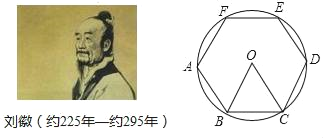
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A是函数y=![]() (x>0)上一动点,连接OA,线段OB与OA关于y轴对称,将线段OA绕点O逆时针旋转90°得线段OC,将线段OA绕点A逆时针旋转90°得线段DA.
(x>0)上一动点,连接OA,线段OB与OA关于y轴对称,将线段OA绕点O逆时针旋转90°得线段OC,将线段OA绕点A逆时针旋转90°得线段DA.

(1)在图1中画出线段OB、OC,保留作图痕迹;
(2)连接AB、BC、AC,当△AOB的面积等于△BOC的面积时,求△ABC的面积;
(3)如图3,若点D的坐标为(m,n),直接写出m与n的等量关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() 是
是![]() 的切线;
的切线;![]() 交
交![]() 于点
于点![]() .
.
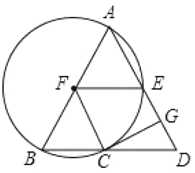
(1)求证:![]() ;
;
(2)填空:①若![]() 的面积为
的面积为![]() ,则
,则![]() 的面积为 ;
的面积为 ;
②当![]() 的度数为 时,四边形
的度数为 时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“创全国文明城市”活动中,某社区为了了解居民掌握垃圾分类知识的情况进行调查.其中A、B两小区分别有500名居民,社区从中各随机抽取50名居民进行相关知识测试,并将成绩进行整理得到部分信息:
(信息一)A小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值);
(信息二)图中,从左往右第四组的成绩如下
75 | 75 | 79 | 79 | 79 | 79 | 80 | 80 |
81 | 82 | 82 | 83 | 83 | 84 | 84 | 84 |
(信息三)A、B两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 方差 |
A | 75.1 | 79 | 40% | 277 | |
B | 75.1 | 77 | 76 | 45% | 211 |
根据以上信息,回答下列问题:
(1)求A小区50名居民成绩的中位数.
(2)请估计A小区500名居民中能超过平均数的有多少人?
(3)请尽量从多个角度比较、分析A,B两小区居民掌握垃圾分类知识的情况.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是__________.
的取值范围是__________.
(2)下表列出了![]() 与
与![]() 的几组对应值,请写出
的几组对应值,请写出![]() ,
,![]() 的值:
的值:![]() ________,
________,![]() ________.
________.
| … |
|
|
|
|
|
|
| 1 | 2 | 3 | 4 | … |
| … |
|
|
|
|
|
|
| 2 |
|
|
| … |
(3)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象.
中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象.
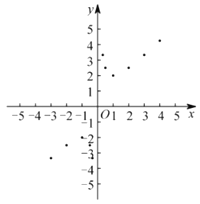
(4)结合函数的图象,请完成:
①当![]() 时,
时,![]() ________;
________;
②写出该函数的一条性质______________________________;
③若方程![]() 有两个相等的实数根,则
有两个相等的实数根,则![]() 的值是____________.
的值是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“分块计数法”:对有规律的图形进行计数时,有些题可以采用“分块计数”的方法.
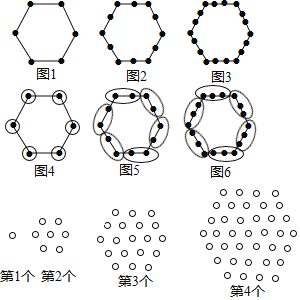
例如:图1有6个点,图2有12个点,图3有18个点,……,按此规律,求图10、图n有多少个点?
我们将每个图形分成完全相同的6块,每块黑点的个数相同(如图),这样图1中黑点个数是6×1=6个;图2中黑点个数是6×2=12个:图3中黑点个数是6×3=18个;所以容易求出图10、图n中黑点的个数分别是 、 .
请你参考以上“分块计数法”,先将下面的点阵进行分块(画在答题卡上),再完成以下问题:
(1)第5个点阵中有 个圆圈;第n个点阵中有 个圆圈.
(2)小圆圈的个数会等于271吗?如果会,请求出是第几个点阵.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级有 ![]() 名学生,在体育考试前随机抽取部分学生进行跳绳测试,根据测试成绩制作了下面两个不完整的统计图.请根据相关信息,解答下列问题:
名学生,在体育考试前随机抽取部分学生进行跳绳测试,根据测试成绩制作了下面两个不完整的统计图.请根据相关信息,解答下列问题:
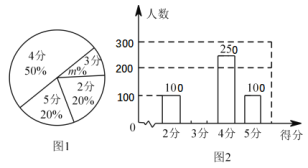
(1)本次参加跳绳测试的学生人数为 ,图 ![]() 中
中 ![]() 的值为 ;
的值为 ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校九年级跳绳测试中得 ![]() 分的学生约有多少人?
分的学生约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com