
ЁОЬтФПЁПаЁУїИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдКЏЪ§![]() ЕФЭМЯѓгыаджЪНјааСЫЬНОПЃЎ
ЕФЭМЯѓгыаджЪНјааСЫЬНОПЃЎ
ЯТУцЪЧаЁУїЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃК
ЃЈ1ЃЉКЏЪ§![]() ЕФздБфСП
ЕФздБфСП![]() ЕФШЁжЕЗЖЮЇЪЧ__________ЃЎ
ЕФШЁжЕЗЖЮЇЪЧ__________ЃЎ
ЃЈ2ЃЉЯТБэСаГіСЫ![]() гы
гы![]() ЕФМИзщЖдгІжЕЃЌЧыаДГі
ЕФМИзщЖдгІжЕЃЌЧыаДГі![]() ЃЌ
ЃЌ![]() ЕФжЕЃК
ЕФжЕЃК![]() ________ЃЌ
________ЃЌ![]() ________ЃЎ
________ЃЎ
| Ё |
|
|
|
|
|
|
| 1 | 2 | 3 | 4 | Ё |
| Ё |
|
|
|
|
|
|
| 2 |
|
|
| Ё |
ЃЈ3ЃЉШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌУшГіСЫвдЩЯБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЎИљОнУшГіЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЎ
жаЃЌУшГіСЫвдЩЯБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЎИљОнУшГіЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЎ
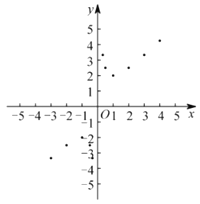
ЃЈ4ЃЉНсКЯКЏЪ§ЕФЭМЯѓЃЌЧыЭъГЩЃК
ЂйЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ________ЃЛ
________ЃЛ
ЂкаДГіИУКЏЪ§ЕФвЛЬѕаджЪ______________________________ЃЛ
ЂлШєЗНГЬ![]() гаСНИіЯрЕШЕФЪЕЪ§ИљЃЌдђ
гаСНИіЯрЕШЕФЪЕЪ§ИљЃЌдђ![]() ЕФжЕЪЧ____________ЃЎ
ЕФжЕЪЧ____________ЃЎ
ЁОД№АИЁП(1)xЁй0ЃЛЃЈ2ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ3ЃЉМћНтЮіЃЛЃЈ4ЃЉtЃО2ЛђtЃМ-2ЃЎ
ЃЛЃЈ3ЃЉМћНтЮіЃЛЃЈ4ЃЉtЃО2ЛђtЃМ-2ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩxдкЗжФИЩЯЃЌПЩЕУГіxЁй0ЃЛ
ЃЈ2ЃЉЗжБ№НЋxЃН![]() КЭx=3ДњШыДњЪ§ЪНЧѓЕУyЕФжЕЃЌМДЗжБ№ЮЊmЁЂnЕФжЕ
КЭx=3ДњШыДњЪ§ЪНЧѓЕУyЕФжЕЃЌМДЗжБ№ЮЊmЁЂnЕФжЕ
ЃЈ3ЃЉНЋЫљИјЕФЕуСЌГЩЯпЃЌМДПЩЛГіКЏЪ§ЭМЯёЃЛ
ЃЈ4ЃЉЂйНЋ![]() ДњШы
ДњШы![]() ЧѓЕУxМДПЩЃЛ
ЧѓЕУxМДПЩЃЛ
ЂкЙлВьКЏЪ§ЭМЯёаДГЩвЛИіЖўДЮКЏЪ§ЭМЯёЕФаджЪМДПЩЃЛ
ЂлНЋ![]() ЛЏГЩвЛдЊЖўДЮЗНГЬЕФвЛАуЪНЃЌШЛКѓгУИљЕФХаБ№ЪНМДПЩНтД№ЃЎ
ЛЏГЩвЛдЊЖўДЮЗНГЬЕФвЛАуЪНЃЌШЛКѓгУИљЕФХаБ№ЪНМДПЩНтД№ЃЎ
НтЃКЃЈ1ЃЉЁпxдкЗжФИЩЯЃЌ
ЁрxЁй0
ЙЪД№АИЮЊЃКxЁй0ЃЛ
ЕБx=3ЪБЃЌ![]() y=x+1ЁСN10
y=x+1ЁСN10
ЃЈ2ЃЉЕБx=![]() ЪБЃЌ
ЪБЃЌ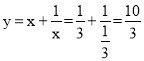 ЃЛ
ЃЛ
ЕБx=3ЪБЃЌ![]() ЃЛ
ЃЛ
ЙЪД№АИЮЊЃК![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉШчЭМЃКСЌЕуГЩЯпЃЌЛГіКЏЪ§ЭМЯёМДПЩЃЛ
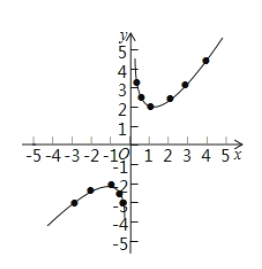
ЃЈ4ЃЉЂйЕБy=![]() ЪБЃЌга
ЪБЃЌга![]() НтЕУЃКx1=2ЃЌx2=
НтЕУЃКx1=2ЃЌx2=![]() ;ЙЪД№АИЮЊЃК2Лђ
;ЙЪД№АИЮЊЃК2Лђ![]() ЃЛ
ЃЛ
ЂкЙлВьКЏЪ§ЭМЯѓЃЌПЩвдЗЂЯжКЏЪ§ЭМЯѓдкЕквЛЁЂШ§ЯѓЯоЧвЙигкдЕуЖдГЦЃЛЙЪД№АИЮЊКЏЪ§ЭМЯѓдкЕквЛЁЂШ§ЯѓЯоЧвЙигкдЕуЖдГЦЃЛ
ЂлЁп![]()
Ёр![]()
гЩЬтвтЕУЃКЁї=t2-4ЃО0ЃЌНтЕУtЃО2ЛђtЃМ-2
ЙЪД№АИЮЊЃКtЃО2ЛђtЃМ-2ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
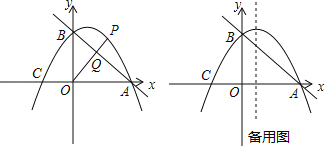
ЁОЬтФПЁПШчЭМЃЌжБЯпy=Љ![]() x+3гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЎХзЮяЯпy=Љ
x+3гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЎХзЮяЯпy=Љ![]() x2+bx+cОЙ§AЁЂBСНЕуЃЌгыxжсЕФСэвЛИіНЛЕуЮЊCЃЎ
x2+bx+cОЙ§AЁЂBСНЕуЃЌгыxжсЕФСэвЛИіНЛЕуЮЊCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуPЪЧЕквЛЯѓЯоХзЮяЯпЩЯЕФЕуЃЌСЌНгOPНЛжБЯпABгкЕуQЃЎЩшЕуPЕФКсзјБъЮЊmЃЌPQгыOQЕФБШжЕЮЊyЃЌЧѓyгыmЕФЙиЯЕЪНЃЌВЂЧѓГіPQгыOQЕФБШжЕЕФзюДѓжЕЃЛ
ЃЈ3ЃЉЕуDЪЧХзЮяЯпЖдГЦжсЩЯЕФвЛЖЏЕуЃЌСЌНгODЁЂCDЃЌЩшЁїODCЭтНгдВЕФдВаФЮЊMЃЌЕБsinЁЯODCЕФжЕзюДѓЪБЃЌЧѓЕуMЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
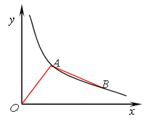
ЁОЬтФПЁПШчЭМЃЌЫЋЧњЯпy=![]() (x>0)ОЙ§AЁЂBСНЕуЃЌШєЕуAЕФКсзјБъЮЊ1ЃЌЁЯOAB=90ЁуЃЌЧвOA=ABЃЌдђkЕФжЕЮЊ________ЃЎ
(x>0)ОЙ§AЁЂBСНЕуЃЌШєЕуAЕФКсзјБъЮЊ1ЃЌЁЯOAB=90ЁуЃЌЧвOA=ABЃЌдђkЕФжЕЮЊ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
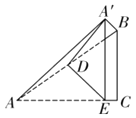
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌЕу
ЕФжаЕуЃЌЕу![]() дкБп
дкБп![]() ЩЯЃЌНЋ
ЩЯЃЌНЋ![]() би
би![]() ЗелЃЌЪЙЕу
ЗелЃЌЪЙЕу![]() ТфдкЕу
ТфдкЕу![]() ДІЃЌСЌНг
ДІЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌЕБ
ЃЌЕБ![]() ЪЧЕШбќжБНЧШ§НЧаЮЪБЃЌ
ЪЧЕШбќжБНЧШ§НЧаЮЪБЃЌ![]() ЕФГЄЮЊ________ЃЎ
ЕФГЄЮЊ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЭМ1жааЁКкЕуЕФИіЪ§МЧЮЊ![]() ЃЌЭМ2жааЁКкЕуЕФИіЪ§МЧЮЊ
ЃЌЭМ2жааЁКкЕуЕФИіЪ§МЧЮЊ![]() ЃЌЭМ3жааЁКкЕуЕФИіЪ§МЧЮЊ
ЃЌЭМ3жааЁКкЕуЕФИіЪ§МЧЮЊ![]() ЃЌЁ
ЃЌЁ
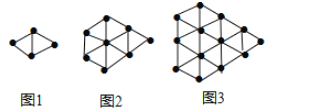
ИљОнвдЩЯЭМжаЕФЙцТЩЭъГЩЯТСаЮЪЬтЃК
ЃЈ1ЃЉЭМ4жааЁКкЕуЕФИіЪ§МЧЮЊ![]() ЃЌдђ
ЃЌдђ![]() __________ЃЛ
__________ЃЛ
ЃЈ2ЃЉЭМ![]() жааЁКкЕуЕФИіЪ§МЧЮЊ
жааЁКкЕуЕФИіЪ§МЧЮЊ![]() ЃЌдђ
ЃЌдђ![]() ___________ЃЈгУКЌ
___________ЃЈгУКЌ![]() ЕФЪНзгБэЪОЃЉЃЛ
ЕФЪНзгБэЪОЃЉЃЛ
ЃЈ3ЃЉШєЕк![]() ИіЭМаЮжааЁКкЕуЕФИіЪ§БШЫќЧАвЛИіЭМаЮжааЁКкЕуЕФИіЪ§Жр100ЃЌдђ
ИіЭМаЮжааЁКкЕуЕФИіЪ§БШЫќЧАвЛИіЭМаЮжааЁКкЕуЕФИіЪ§Жр100ЃЌдђ![]() ЕФжЕЪЧЖрЩйЃП
ЕФжЕЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪмвцгкЙњМвжЇГжаТФмдДЦћГЕЗЂеЙКЭЁАвЛДјвЛТЗЁБЗЂеЙеНТдЕШЖржиРћКУвђЫиЃЌЮвЪаФГЦћГЕСуВПМўЩњВњЦѓвЕЕФРћШѓж№ФъЬсИпЃЌОнЭГМЦЃЌ2016ФъРћШѓЮЊ3вкдЊЃЌ2018ФъРћШѓЮЊ4.32вкдЊЃЎ
ЃЈ1ЃЉЧѓИУЦѓвЕДг2016ФъЕН2018ФъРћШѓЕФФъЦНОљдіГЄТЪЃЛ
ЃЈ2ЃЉШє2019ФъБЃГжЧАСНФъРћШѓЕФФъЦНОљдіГЄТЪВЛБфЃЌИУЦѓвЕ2019ФъЕФРћШѓФмЗёГЌЙ§5вкдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
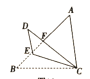
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎдђ
ЃЎдђ![]() ЕФГЄЮЊ__________ЃЛШє
ЕФГЄЮЊ__________ЃЛШє![]() ЪЧ
ЪЧ![]() БпЩЯвЛЕуЃЌНЋ
БпЩЯвЛЕуЃЌНЋ![]() би
би![]() ЫљдкжБЯпЗелЕУЕН
ЫљдкжБЯпЗелЕУЕН![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гк
гк![]() ЃЌдђЕБ
ЃЌдђЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФжЕЮЊ__________ЃЎ
ЕФжЕЮЊ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
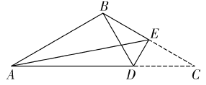
ЁОЬтФПЁПШчЭМЃЌдкЕШбќШ§НЧаЮжНЦЌ![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЗжБ№дкБп
ЗжБ№дкБп![]() ЩЯЃЌСЌНг
ЩЯЃЌСЌНг![]() ЃЌНЋ
ЃЌНЋ![]() би
би![]() ЗелЪЙЕУЕу
ЗелЪЙЕУЕу![]() ЧЁКУТфдкЕу
ЧЁКУТфдкЕу![]() ДІЃЌдђ
ДІЃЌдђ![]() ЕФГЄЮЊЃЈ ЃЉ
ЕФГЄЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com