
【题目】小明想要测量水面人工岛上两棵小树CD的距离,如图,已知河岸MN∥CD,小明在河岸MN上点A处测量小树C位于北偏东60°方向,然后沿河岸走了20米,到达点B处,此时测得河对岸小树C位于北偏东30°方向,小树D位于东北方向,则两棵树CD的距离为_____米.(结果保留根号)
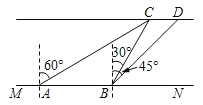
【答案】(10![]() ﹣10)
﹣10)
【解析】
作CE⊥MN于点E、DF⊥MN于点F,设BE=a,利用三角函数求得![]() ,再由tan∠CAE=
,再由tan∠CAE=![]() 列方程求得a=10,据此知BE=10,DF=CE=10
列方程求得a=10,据此知BE=10,DF=CE=10![]() ,继而由∠DBF=45°知BF=DF=10
,继而由∠DBF=45°知BF=DF=10![]() ,从而得出答案.
,从而得出答案.
如图所示,过点C作CE⊥MN于点E,过点D作DF⊥MN于点F,
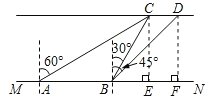
设BE=a,
在Rt△BCE中,∵∠BCE=30°,
∴CE=![]() =
=![]() =
=![]() a,
a,
在Rt△ACE中,∵∠CAE=30°,AB=20,
∴由tan∠CAE=![]() 可得
可得![]() =
=![]() ,
,
解得a=10,
∴BE=10,DF=CE=10![]() ,
,
在Rt△BDF中,∵∠DBF=45°,
∴BF=DF=10![]() ,
,
∴CD=EF=BF﹣BE=10![]() ﹣10(米),
﹣10(米),
故答案为:(10![]() ﹣10).
﹣10).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】东北大米主要种植于黑龙江省、吉林省、辽宁省的广大平原地区,种植在极其肥沃的黑土地中,吸收了足够的氮、磷、钾等多种矿物元素,阳光雨露充足,又有纯净无污染的灌溉用水,生长周期比较长,一般五个月左右.东北大米颗粒饱满,质地坚硬,色泽清白透明;饭粒油亮,香味浓郁;蒸煮后出饭率高,粘性较小,米质较脆.刘阿姨到超市购买东北大米,第一次按原价购买,用了105元.几天后,遇上这种大米8折出售,她用140元又买了一些,两次共购买了40kg.这种东北大米的原价是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△MNQ中,MQ≠NQ.
(1)请你以MN为一边,在MN的同侧构造一个与△MNQ全等的三角形,画出图形,并简要说明构造的方法;
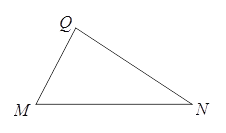
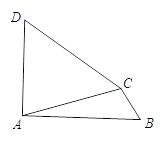
(2)参考(1)中构造全等三角形的方法解决下面问题:
如图,在四边形ABCD中,![]() ,∠B=∠D.求证:CD=AB.
,∠B=∠D.求证:CD=AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=kx2+(1﹣2k)x+1﹣3k与x轴有两个不同的交点A、B.
(1)求k的取值范围;
(2)证明该抛物线一定经过非坐标轴上的一点M,并求出点M的坐标;
(3)当![]() <k≤8时,由(2)求出的点M和点A,B构成的△ABM的面积是否有最值?若有,求出该最值及相对应的k值.
<k≤8时,由(2)求出的点M和点A,B构成的△ABM的面积是否有最值?若有,求出该最值及相对应的k值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.
(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并猜测∠FCN的度数,并说明理由;
(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=a,BC=b(a、b为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变?若∠FCN的大小不变,请用含a、b的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请举例说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖公司准备运送152箱小龙虾到A、B两地销售,该批小龙虾刚好能用大小货车15辆一次运完,已知大货车每辆能装12箱,小货车每辆能装8箱,其中每辆大货车运往A、B两地的运费分别为800元和900元;每辆小货车运往A、B两地的运费分别为400元和600元.
(1)求这15辆车中大小货车各有多少辆?
(2)现安排其中10辆货车前往A地,其余货车前往B地,设前往A地的大货车为m辆,前往A、B两地总费用为y元,试求出y与m的函数解析式,并写出m的取值范围;
(3)在(2)的条件下,若运往B地的费用不高于A地费用的一半,求此时的最低总运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年5月26日第5届中国国际大数据产业博览会召开.某市在五届数博会上的产业签约金额的折线统计图如图.下列说法正确的是( )

A. 签约金额逐年增加
B. 与上年相比,2019年的签约金额的增长量最多
C. 签约金额的年增长速度最快的是2016年
D. 2018年的签约金额比2017年降低了22.98%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() ,对称轴交
,对称轴交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,交抛物线的对称轴于点
,交抛物线的对称轴于点![]() .
.
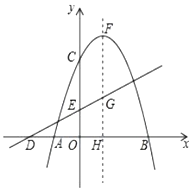
(1)求出![]() 的值.
的值.
(2)点![]() 为抛物线上一个动点,当点
为抛物线上一个动点,当点![]() 关于直线
关于直线![]() 的对称点恰好落在
的对称点恰好落在![]() 轴上时,请直接写出此时点
轴上时,请直接写出此时点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】身高1.65米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形CDEF代表建筑物,兵兵位于建筑物前点B处,风筝挂在建筑物上方的树枝点G处(点G在FE的延长线上).经测量,兵兵与建筑物的距离BC=5米,建筑物底部宽FC=7米,风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上,点A距地面的高度AB=1.4米,风筝线与水平线夹角为37°.
(1)求风筝距地面的高度GF;
(2)在建筑物后面有长5米的梯子MN,梯脚M在距墙3米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根米长的竹竿能否触到挂在树上的风筝?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com