
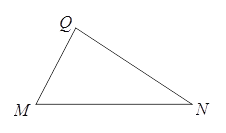
【题目】已知:如图,△MNQ中,MQ≠NQ.
(1)请你以MN为一边,在MN的同侧构造一个与△MNQ全等的三角形,画出图形,并简要说明构造的方法;
(2)参考(1)中构造全等三角形的方法解决下面问题:
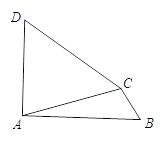
如图,在四边形ABCD中,![]() ,∠B=∠D.求证:CD=AB.
,∠B=∠D.求证:CD=AB.
【答案】(1)作图见解析;(2)证明书见解析.
【解析】
试题(1)以点N为圆心,以MQ长度为半径画弧,以点M为圆心,以NQ长度为半径画弧,两弧交于一点F,则△MNF为所画三角形.
(2)延长DA至E,使得AE=CB,连结CE.证明△EAC≌△BCA,得:∠B =∠E,AB=CE,根据等量代换可以求得答案.
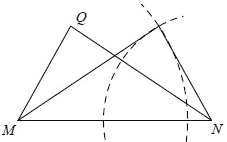
试题解析:(1)如图1,以N 为圆心,以MQ 为半径画圆弧;以M 为圆心,以NQ 为半径画圆弧;两圆弧的交点即为所求.
(2)如图,延长DA至E,使得AE=CB,连结CE.
∵∠ACB +∠CAD =180°,∠DACDAC +∠EAC =180°,∴∠BACBCA =∠EAC.
在△EAC和△BAC中,AE=CE,AC=CA,∠EAC=∠BCN,
∴△AECEAC≌△BCA (SAS).∴∠B=∠E,AB=CE.
∵∠B=∠D,∴∠D=∠E.∴CD=CE,∴CD=AB.



科目:初中数学 来源: 题型:
【题目】如图,AD是圆O的切线,切点为A,AB是圆O的弦。过点B作BC//AD,交圆O于点C,连接AC,过点C作CD//AB,交AD于点D。连接AO并延长交BC于点M,交过点C的直线于点P,且BCP=ACD。
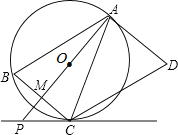
(1)判断直线PC与圆O的位置关系,并说明理由:
(2) 若AB=9,BC=6,求PC的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
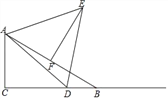
【题目】在Rt△ABC中,∠C=90°,∠B=30°,AB=10,点D是射线CB上的一个动点,△ADE是等边三角形,点F是AB的中点,连接EF.
(1)如图,点D在线段CB上时,
①求证:△AEF≌△ADC;
②连接BE,设线段CD=x,BE=y,求y2﹣x2的值;
(2)当∠DAB=15°时,求△ADE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求tan∠BAF的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,AB是⊙O的直径,G为弦AE的中点,连接OG并延长交⊙O于点D,连接BD交AE于点F,延长AE至点C,使得FC=BC,连接BC.
(1)求证:BC是⊙O的切线;
(2)⊙O的半径为5,tanA=![]() ,求FD的长.
,求FD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
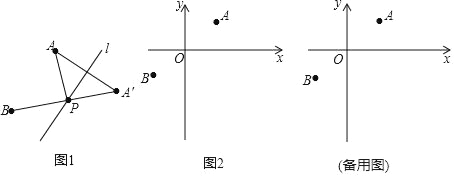
【题目】(定义)如图1,A,B为直线l同侧的两点,过点A作直线1的对称点A′,连接A′B交直线l于点P,连接AP,则称点P为点A,B关于直线l的“等角点”.
(运用)如图2,在平面直坐标系xOy中,已知A(2,![]() ),B(﹣2,﹣
),B(﹣2,﹣![]() )两点.
)两点.
(1)C(4,![]() ),D(4,
),D(4,![]() ),E(4,
),E(4,![]() )三点中,点 是点A,B关于直线x=4的等角点;
)三点中,点 是点A,B关于直线x=4的等角点;
(2)若直线l垂直于x轴,点P(m,n)是点A,B关于直线l的等角点,其中m>2,∠APB=α,求证:tan![]() =
=![]() ;
;
(3)若点P是点A,B关于直线y=ax+b(a≠0)的等角点,且点P位于直线AB的右下方,当∠APB=60°时,求b的取值范围(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
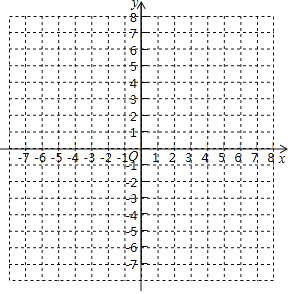
【题目】在平面直角坐标系xOy中,点A在第一象限,点A,B关于y轴对称.
(1)若A(1,3),写出点B的坐标并在直角坐标系中标出.
(2)若A(a,b),且△AOB的面积为a2,求点B的坐标(用含a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在南开中学校庆78周年之际,由学生处和美术教研组共同策划、组织了“南开中学校园明信片设计大赛”。获得此次设计大赛组织一等奖的![]() 、
、![]() 、
、![]() 、
、![]() 四个班级一共有75件作品获奖,已知
四个班级一共有75件作品获奖,已知![]() 班参赛作品的获奖率为30%,
班参赛作品的获奖率为30%,![]() 班参赛作品的获奖率为40%。请结合两幅统计图所提供的信息,解决下列问题:
班参赛作品的获奖率为40%。请结合两幅统计图所提供的信息,解决下列问题: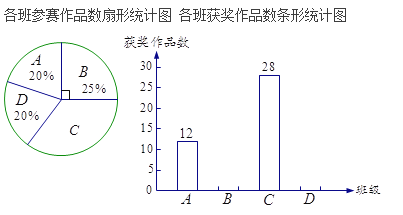
(1)四个班级一共选送了多少件作品参赛,获奖率最高的班级是哪个班;
(2)请将条形统计图补充完整;
(3)![]() 班的小欣和小怡同学在本次大赛中荣获个人一等奖,此外
班的小欣和小怡同学在本次大赛中荣获个人一等奖,此外![]() 、
、![]() 两班各有一名同学荣获个人一等奖。南开中学校友会准备从这4名同学的作品中任选两件,制作成新年贺卡送给老校友。请用列表法或画树状图的方法求出这两件作品分别来自不同班级,且其中一件是小欣或小怡作品的概率.
两班各有一名同学荣获个人一等奖。南开中学校友会准备从这4名同学的作品中任选两件,制作成新年贺卡送给老校友。请用列表法或画树状图的方法求出这两件作品分别来自不同班级,且其中一件是小欣或小怡作品的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若两个分式的和为![]() (
(![]() 为正整数),则称这两个分式互为“
为正整数),则称这两个分式互为“![]() 阶分式”,例如分式
阶分式”,例如分式![]() 与
与![]() 互为“3阶分式”.
互为“3阶分式”.
(1)分式![]() 与 互为“5阶分式”;
与 互为“5阶分式”;
(2)设正数![]() 互为倒数,求证:分式
互为倒数,求证:分式![]() 与
与![]() 互为“2阶分式”;
互为“2阶分式”;
(3)若分式![]() 与
与![]() 互为“1阶分式”(其中
互为“1阶分式”(其中![]() 为正数),求
为正数),求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com