
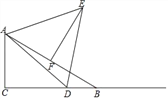
【题目】在Rt△ABC中,∠C=90°,∠B=30°,AB=10,点D是射线CB上的一个动点,△ADE是等边三角形,点F是AB的中点,连接EF.
(1)如图,点D在线段CB上时,
①求证:△AEF≌△ADC;
②连接BE,设线段CD=x,BE=y,求y2﹣x2的值;
(2)当∠DAB=15°时,求△ADE的面积.
【答案】(1)①证明见解析;②25;(2)为![]() 或50
或50![]() +75..
+75..
【解析】
试题(1)、①在直角三角形ABC中,由30°所对的直角边等于斜边的一半求出AC的长,再由F为AB中点,得到AC=AF=5,确定出三角形ADE为等边三角形,利用等式的性质得到一对角相等,再由AD=AE,利用SAS即可得证;②由全等三角形对应角相等得到∠AEF为直角,EF=CD=x,在三角形AEF中,利用勾股定理即可列出y关于x的函数解析式;(2)、分两种情况考虑:①当点在线段CB上时;②当点在线段CB的延长线上时,分别求出三角形ADE面积即可.
试题解析:(1)、①证明:在Rt△ABC中,∵∠B=30°,AB=10,
∴∠CAB=60°,AC=![]() AB=5, ∵点F是AB的中点, ∴AF=
AB=5, ∵点F是AB的中点, ∴AF=![]() AB=5,
AB=5,
∴AC=AF, ∵△ADE是等边三角形, ∴AD=AE,∠EAD=60°, ∵∠CAB=∠EAD,
即∠CAD+∠DAB=∠FAE+∠DAB, ∴∠CAD=∠FAE, ∴△AEF≌△ADC(SAS);
②∵△AEF≌△ADC,∴∠AEF=∠C=90°,EF=CD=x,又∵点F是AB的中点,
∴AE=BE=y, 在Rt△AEF中,勾股定理可得:y2=25+x2, ∴y2﹣x2=25
(2)①当点在线段CB上时, 由∠DAB=15°,可得∠CAD=45°,△ADC是等腰直角三角形,
∴AD2=50, △ADE的面积为![]() ;
;
②当点在线段CB的延长线上时, 由∠DAB=15°,可得∠ADB=15°,BD=BA=10,
∴在Rt△ACD中,勾股定理可得AD2=200+100![]() , △ADE的面积为50
, △ADE的面积为50 ![]() +75,
+75,
综上所述,△ADE的面积为![]() 或50
或50 ![]() +75.
+75.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA=2,将菱形OABC绕原点顺时针旋转105°至OA′B′C′的位置,则点B′的坐标为( )

A. (![]() ,
,![]() ) B. (
) B. (![]() ,
,![]() ) C. (2,-2) D. (
) C. (2,-2) D. (![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年11月20日-23日,首届世界![]() 大会在北京举行.某校的学生开展对于
大会在北京举行.某校的学生开展对于![]() 知晓情况的问卷调查,问卷调查的结果分为
知晓情况的问卷调查,问卷调查的结果分为![]() 、
、![]() 、
、![]() 、
、![]() 四类,其中
四类,其中![]() 类表示“非常了解”,
类表示“非常了解”,![]() 类表示“比较了解”,
类表示“比较了解”,![]() 类表示“基本了解”,
类表示“基本了解”,![]() 类表示“不太了解”,并把调查结果绘制成如图所示的两个统计图表(不完整).
类表示“不太了解”,并把调查结果绘制成如图所示的两个统计图表(不完整).

根据上述信息,解答下列问题:
(1)这次一共调查了多少人;
(2)求“![]() 类”在扇形统计图中所占圆心角的度数;
类”在扇形统计图中所占圆心角的度数;
(3)请将条形统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的方程x2﹣(2m+1)x+2m=0
(1)求证:方程一定有两个实数根;
(2)若方程的两根为x1,x2,且|x1|=|x2|,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )

A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点D、点E为BC边上两点,且AC=DC,
(1)若∠EAC=∠EAF,EF⊥AB且AB=5,BC=4,求线段DE的长度;
(2)若EF⊥AD于点P,CF⊥AE于点Q,且AE=CF,求证:![]() DE+PF=AP
DE+PF=AP

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店老板第一次用1000元购进一批文具,很快销售完毕;第二次购进时发现每件文具进价比第一次上涨了2 5元.老板用2500元购进了第二批文具,所购进文具的数量是第一次购进数量的2倍,同样很快销售完毕,两批文具的售价均为每件15元.
(1)问第二次购进了多少件文具?
(2)文具店老板第一次购进的文具有3% 的损耗,第二次购进的文具有5% 的损耗,问文具店老板在这两笔生意中是盈利还是亏本?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:矩形ABCD中,AB=4,BC=3,点M、N分别在边AB、CD上,直线MN交矩形对角线 AC于点E,将△AME沿直线MN翻折,点A落在点P处,且点P在射线CB上.
(1)如图1,当EP⊥BC时,求CN的长;
(2) 如图2,当EP⊥AC时,求AM的长;
(3) 请写出线段CP的长的取值范围,及当CP的长最大时MN的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com