
【题目】如图,在△ABC中,∠C=90°,点D、点E为BC边上两点,且AC=DC,
(1)若∠EAC=∠EAF,EF⊥AB且AB=5,BC=4,求线段DE的长度;
(2)若EF⊥AD于点P,CF⊥AE于点Q,且AE=CF,求证:![]() DE+PF=AP
DE+PF=AP

【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)由勾股定理可求AC=3,由“AAS”可证△ACE≌△AFE,可得AC=AF=3,EC=EF,由勾股定理可求CE的长,即可求DE的长;
(2)如图,连接DF,由“SAS”可证△ACE≌△CDF,可得CE=DF,∠ACE=∠CDF=90°,设AC=CD=2a,由等腰直角三角形的性质可得AD=2![]() a,EC=DF=DE=a,EF=
a,EC=DF=DE=a,EF=![]() a,DP=EP=PF=
a,DP=EP=PF=![]() a,即可得结论.
a,即可得结论.
解:∵AB=5,BC=4,∠C=90°,
∴AC=![]() =3,
=3,
∵AE=AE,∠EAC=∠EAF,∠C=∠EFA=90°,
∴△ACE≌△AFE(AAS)
∴AC=AF=3,EC=EF,
∴CD=AC=3,BF=2,
∵BE2=BF2+EF2,
∴BE2=4+(4﹣BE)2,
∴BE=![]() ,
,
∴EC=![]() ,
,
∴DE=CD﹣CE=![]() ;
;
(2)如图,连接DF,
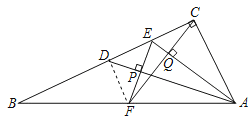
∵CF⊥AE,
∴∠ACB=∠CQA=90°
∴∠ACQ+∠ECQ=90°,∠ACQ+∠CAQ=90°,
∴∠ECQ=∠CAQ,且CD=AC,CF=AE,
∴△ACE≌△CDF(SAS)
∴CE=DF,∠ACE=∠CDF=90°,
∵AC=CD,∠ACD=90°,
∴∠CAD=∠CDA=45°,
∴∠FDA=∠CDA=45°,且EF⊥AD,
∴∠EDP=∠DEP=45°=∠PDF=∠DFP,
∴DP=PE=PF,DF=DE,
∴DE=DF=EC,
设AC=CD=2a,
∴AD=2![]() a,EC=DF=DE=a,
a,EC=DF=DE=a,
∴EF=![]() a,DP=EP=PF=
a,DP=EP=PF=![]() a,
a,
∴AP=AD﹣DP=![]() a,
a,
∴![]() DE+PF=
DE+PF=![]() a+
a+![]() a=
a=![]() a=AP
a=AP
∴![]() DE+PF=AP.
DE+PF=AP.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△OAB中,OA=OB=10,∠AOB=80°,以点O为圆心,6为半径的优弧弧MN分别交OA、OB于点M,N.
(1)点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转80°得![]() ,求证:AP=BP;
,求证:AP=BP;
(2)点T在左半弧上,若AT与弧相切,求点T到OA的距离;
(3)设点Q在优弧弧MN上,当△AOQ的面积最大时,直接写出∠BOQ的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州瓯柑,声名远播.某经销商欲将仓库的120吨瓯柑运往A,B两地销售.运往A,B两地的瓯柑(吨)和每吨的运费如下表.设仓库运往A地的瓯柑为x吨,且x为整数.
瓯柑(吨) | 运费(元/吨) | |
A地 | x | 20 |
B地 | 30 |
(1)设仓库运往A,B两地的总运费为y元.
①将表格补充完整.
②求y关于x的函数表达式.
(2)若仓库运往A地的费用不超过运往A,B两地费用的![]() ,求总运费的最小值.
,求总运费的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
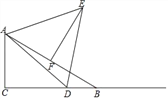
【题目】在Rt△ABC中,∠C=90°,∠B=30°,AB=10,点D是射线CB上的一个动点,△ADE是等边三角形,点F是AB的中点,连接EF.
(1)如图,点D在线段CB上时,
①求证:△AEF≌△ADC;
②连接BE,设线段CD=x,BE=y,求y2﹣x2的值;
(2)当∠DAB=15°时,求△ADE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售![]() ,
,![]() 两种型号的新能源汽车。上周售出1辆
两种型号的新能源汽车。上周售出1辆![]() 型车和3辆
型车和3辆![]() 型车,销售额为96万元,本周已售出2辆
型车,销售额为96万元,本周已售出2辆![]() 型车和1辆
型车和1辆![]() 型车,销售额为62万元。
型车,销售额为62万元。
(1)求每辆![]() 型车和
型车和![]() 型车的售价各为多少?
型车的售价各为多少?
(2)随着汽车限购政策的推行,预计下周起![]() ,
,![]() 两种型号的汽车价格在原有的基础均有上涨,若
两种型号的汽车价格在原有的基础均有上涨,若![]() 型汽车价格上涨m%,
型汽车价格上涨m%,![]() 型汽车价格上涨3m%,则同时购买一台
型汽车价格上涨3m%,则同时购买一台![]() 型车和一台
型车和一台![]() 型车的费用比涨价前多12%,求
型车的费用比涨价前多12%,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中有三点A(﹣2,1)、B(3,1)、C(2,3).请回答如下问题:
(1)在坐标系内描出点A、B、C的位置,并求△ABC的面积;
(2)在平面直角坐标系中画出△A′B′C′,使它与△ABC关于x轴对称,并写出△A′B′C′三顶点的坐标;
(3)若M(x,y)是△ABC内部任意一点,请直接写出这点在△A′B′C′内部的对应点M′的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ADB、△BCD都是等边三角形,点E,F分别是AB,AD上两个动点,满足AE=DF.连接BF与DE相交于点G,CH⊥BF,垂足为H,连接CG.若DG=![]() ,BG=
,BG=![]() ,且
,且![]() 、
、![]() 满足下列关系:
满足下列关系:![]() ,
,![]() ,则GH= .
,则GH= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,BD=8.
(1)求证:四边形ABCD是菱形;
(2)过点A作AH⊥BC于点H,求AH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,![]() ,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
(1)求∠BAC的度数;
(2)当点D在AB上方,且CD⊥BP时,求证:PC=AC;
(3)在点P的运动过程中
①当点A在线段PB的中垂线上或点B在线段PA的中垂线上时,求出所有满足条件的∠ACD的度数;
②设⊙O的半径为6,点E到直线l的距离为3,连结BD,DE,直接写出△BDE的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com