
【题目】如图,△OAB中,OA=OB=10,∠AOB=80°,以点O为圆心,6为半径的优弧弧MN分别交OA、OB于点M,N.
(1)点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转80°得![]() ,求证:AP=BP;
,求证:AP=BP;
(2)点T在左半弧上,若AT与弧相切,求点T到OA的距离;
(3)设点Q在优弧弧MN上,当△AOQ的面积最大时,直接写出∠BOQ的度数.

【答案】(1)答案见解析;(2)![]() ;(3)当∠BOQ的度数为10°或170°时,△AOQ的面积最大.
;(3)当∠BOQ的度数为10°或170°时,△AOQ的面积最大.
【解析】
试题(1)首先根据已知得出∠AOP=∠BOP′,进而得出△AOP≌△BOP′,即可得出答案;
(2)利用切线的性质得出∠ATO=90°,再利用勾股定理求出AT的长,进而得出TH的长即可得出答案;
(3)当OQ⊥OA时,△AOQ面积最大,且左右两半弧上各存在一点分别求出即可.
试题解析:(1)∵∠AOP=∠AOB+∠BOP=80°+∠BOP,
∠BOP′=∠POP′+∠BOP=80°+∠BOP,
∴∠AOP=∠BOP′,
∵在△AOP和△BOP′中,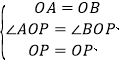 ,
,
∴△AOP≌△BOP′(SAS),
∴AP=BP′;
(2)连接OT,过点T作TH⊥OA于点H,
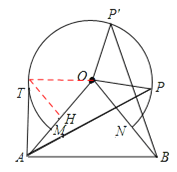
∵AT与⊙O相切,∴∠ATO=90°,
∴AT=![]() =8,
=8,
∵![]() ×OA×TH=
×OA×TH=![]() ×AT×OT,
×AT×OT,
∴![]() ×10×TH=
×10×TH=![]() ×8×6,解得:TH=
×8×6,解得:TH=![]() ,
,
∴点T到OA的距离为![]() ;
;
(3)如图,当OQ⊥OA时,△AOQ的面积最大,理由如下:
当Q点在优弧![]() 左侧上,
左侧上,
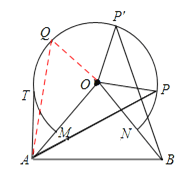
∵OQ⊥OA,
∴QO是△AOQ中最长的高,则△AOQ的面积最大,
∴∠BOQ=∠AOQ+∠AOB=90°+80°=170°,
当Q点在优弧MN右侧上,
∵OQ⊥OA,
∴QO是△AOQ中最长的高,则△AOQ的面积最大,
∴∠BOQ=∠AOQ-∠AOB=90°-80°=10°,
综上所述:当∠BOQ的度数为10°或170°时,△AOQ的面积最大.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
【题目】某中学举行“庆祝中华人民共和国成立70周年”知识预赛,学生会把成绩![]() (分)分成五组:A组:
(分)分成五组:A组:![]() ;B组:
;B组:![]() ;C组:
;C组:![]() ;D组:
;D组:![]() ;E组:
;E组:![]() .
.
统计后绘制成如下两个统计图(不完整).

(1)直接填空:
①![]() 的值为_________;
的值为_________;
②在图2中,![]() 组的扇形圆心角的度数为_________.
组的扇形圆心角的度数为_________.
(2)在图1中,画出![]() 所对应的条形图;
所对应的条形图;
(3)若学生会计划从预赛中选拔前30名进入复赛,则进入复赛的成绩应不低于多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】兴发服装店老板用4500元购进一批某款T恤衫,由于深受顾客喜爱,很快售完,老板又用4950元购进第二批该款式T恤衫,所购数量与第一批相同,但每件进价比第一批多了9元.
(1)第一批该款式T恤衫每件进价是多少元?
(2)老板以每件120元的价格销售该款式T恤衫,当第二批T恤衫售出![]() 时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于650元,剩余的T恤衫每件售价至少要多少元?(利润=售价﹣进价)
时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于650元,剩余的T恤衫每件售价至少要多少元?(利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA=2,将菱形OABC绕原点顺时针旋转105°至OA′B′C′的位置,则点B′的坐标为( )

A. (![]() ,
,![]() ) B. (
) B. (![]() ,
,![]() ) C. (2,-2) D. (
) C. (2,-2) D. (![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:一般地,![]() 个相同的因数
个相同的因数![]() 相乘
相乘 ![]() ,记为
,记为![]() .如
.如![]() ,此时,
,此时,![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记为
的对数,记为![]() (即
(即![]() ).一般地,若
).一般地,若![]() ,(
,(![]() 且
且![]() ,
,![]() ),则
),则![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记为
的对数,记为![]() (即
(即![]() ).如
).如![]() ,则
,则![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记为
的对数,记为![]() (即
(即![]() ).
).
(1)计算以下各对数的值:![]() __________,
__________,![]() __________,
__________,![]() __________.
__________.
(2)观察(1)中三数![]() 、
、![]() ,
,![]() 之间满足怎样的关系式,
之间满足怎样的关系式,![]() 、
、![]() 、
、![]() 之间又满足怎样的关系式;
之间又满足怎样的关系式;
(3)由(2)的结果,你能归纳出一个一般性的结论吗?![]() __________.(
__________.(![]() 且
且![]() ,
,![]() ,
,![]() )
)
(4)根据幂的运算法则:![]() 以及对数的含义证明上述结论.
以及对数的含义证明上述结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列的网格图中.每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.
(1)试在图中作出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(-3,5),试在图中画出直角坐标系,并标出A、C两点的坐标;
(3)根据(2)中的坐标系作出与△ABC关于原点对称的图形△A2B2C2,并标出B2、C2两点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个正整数m能写成m=(a﹣b)(a+b)(a、b均为正整数,且a≠b),则称m为“完美数”,a、b为m的一个完美变形,在m的所有完美变形中,若a2+b2最大,则称a、b为m的最佳完美变形,此时F(m)=a2+b2.例如:12=(4+2)(4﹣2),12为“完美数”,4和2为12的一个完美变形,32=(9+7)(9﹣7)=(6+2)(6﹣2),因为92+72>62+22,所以9和7是32的最佳完美变形,所以F(32)=130.
(1)8 (填“是”或“不是”)完美数;10 (填“是”或“不是”)完美数;13 (填“是”或“不是”)完美数;
(2)求F(48);
(3)若一个两位数n的十位数字和个位数字分别为x,y(1≤x≤y≤9),n为“完美数”且x+y能被8整除,求F(n)的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年11月20日-23日,首届世界![]() 大会在北京举行.某校的学生开展对于
大会在北京举行.某校的学生开展对于![]() 知晓情况的问卷调查,问卷调查的结果分为
知晓情况的问卷调查,问卷调查的结果分为![]() 、
、![]() 、
、![]() 、
、![]() 四类,其中
四类,其中![]() 类表示“非常了解”,
类表示“非常了解”,![]() 类表示“比较了解”,
类表示“比较了解”,![]() 类表示“基本了解”,
类表示“基本了解”,![]() 类表示“不太了解”,并把调查结果绘制成如图所示的两个统计图表(不完整).
类表示“不太了解”,并把调查结果绘制成如图所示的两个统计图表(不完整).

根据上述信息,解答下列问题:
(1)这次一共调查了多少人;
(2)求“![]() 类”在扇形统计图中所占圆心角的度数;
类”在扇形统计图中所占圆心角的度数;
(3)请将条形统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点D、点E为BC边上两点,且AC=DC,
(1)若∠EAC=∠EAF,EF⊥AB且AB=5,BC=4,求线段DE的长度;
(2)若EF⊥AD于点P,CF⊥AE于点Q,且AE=CF,求证:![]() DE+PF=AP
DE+PF=AP

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com