
【题目】一个正整数m能写成m=(a﹣b)(a+b)(a、b均为正整数,且a≠b),则称m为“完美数”,a、b为m的一个完美变形,在m的所有完美变形中,若a2+b2最大,则称a、b为m的最佳完美变形,此时F(m)=a2+b2.例如:12=(4+2)(4﹣2),12为“完美数”,4和2为12的一个完美变形,32=(9+7)(9﹣7)=(6+2)(6﹣2),因为92+72>62+22,所以9和7是32的最佳完美变形,所以F(32)=130.
(1)8 (填“是”或“不是”)完美数;10 (填“是”或“不是”)完美数;13 (填“是”或“不是”)完美数;
(2)求F(48);
(3)若一个两位数n的十位数字和个位数字分别为x,y(1≤x≤y≤9),n为“完美数”且x+y能被8整除,求F(n)的最小值.
【答案】(1)是,不是,是;(2)290;(3)F(n)的最小值为145
【解析】
(1)根据完美数的特征即可得到结论;
(2)设![]() ,根据把48写成两数的乘积,然后分类讨论即可;
,根据把48写成两数的乘积,然后分类讨论即可;
(3)由题可知:n=10x+y=(a+b)(a﹣b).因为x+y能够被8整除且1≤x<y≤9,所以x+y=8或x+y=16,分两种情况讨论即可求解.
解:(1)∵8=(3﹣1)×(3+1),
∴8是完美数;
∵10不能写成两个正整数和与差乘积的形式,
∴10不是完美数;
∵13=(7﹣6)×(7+6),
∴13是完美数.
故答案为:是,不是,是;
(2)设![]()
因为a+b,a﹣b同为奇数或同为偶数,所以48=24×2 或 48=12×4 或48=8×6,
![]() 或
或![]() 或
或![]()
解得:![]() 或
或![]() 或
或![]()
∵132+112>82+42>72+12
∴F(48)=132+112=290
(3)由题可知:n=10x+y=(a+b)(a﹣b).
∵x+y能够被8整除且1≤x<y≤9,
∴x+y=8或x+y=16
①当x+y=8时,1≤x<y≤9,∴x=1或2或3,
即n=17或26或35,而26不是“完美数”
![]() 或
或![]() 或
或![]() ,
,
解得:![]() 或
或![]() 或
或![]() .
.
F(17)=92+82=145,
∵182+172>62+12
∴F(35)=182+172=613
②当x+y=16时,1≤x<y≤9,∴x=7,
∴n=79
∴![]() ,
,
解得![]() ,
,
∴F(79)=402+392=3121,
∴F(n)的最小值为145.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
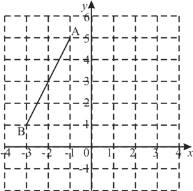
【题目】如图,在平面直角坐标系中,点A的坐标为(﹣1,5),点B的坐标为(﹣3,1).
(1)在平面直角坐标系中作线段AB关于y轴对称的线段A1B1(A与A1,B与B1对应);
(2)求△AA1B1的面积;
(3)在y轴上存在一点P,使PA+PB的值最小,则点P的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新定义:如图(1)和图(2)中,点P是平面内一点,如果![]() =2或
=2或![]() =
=![]() ,称点P是线段AB的强弱点.
,称点P是线段AB的强弱点.
(1)如图2,在Rt△APB中,∠APB=90°,∠A=30°,问:点B是否是线段AP的强弱点?请说明理由;
(2)如图3,在Rt△ABC中,∠ACB=90°,B是线段AC的强弱点(BA>BC),BD是Rt△ABC的角平分线,求证:点D是线段AC上的强弱点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAB中,OA=OB=10,∠AOB=80°,以点O为圆心,6为半径的优弧弧MN分别交OA、OB于点M,N.
(1)点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转80°得![]() ,求证:AP=BP;
,求证:AP=BP;
(2)点T在左半弧上,若AT与弧相切,求点T到OA的距离;
(3)设点Q在优弧弧MN上,当△AOQ的面积最大时,直接写出∠BOQ的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个A奖品和2个B奖品共需130元;购买5个A奖品和4个B奖品共需230元.
(1)求A,B两种奖品的单价;
(2)学校准备购买A,B两种奖品共40个,且A奖品的数量不少于B奖品数量的![]() .购买预算金不超过920元,请问学校有几种购买方案.
.购买预算金不超过920元,请问学校有几种购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=12,BC=8,过对角线BD中点O的直线分别交AB,CD边于点E,F.

(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32,连接BD,AE⊥BD,垂足为E.
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州瓯柑,声名远播.某经销商欲将仓库的120吨瓯柑运往A,B两地销售.运往A,B两地的瓯柑(吨)和每吨的运费如下表.设仓库运往A地的瓯柑为x吨,且x为整数.
瓯柑(吨) | 运费(元/吨) | |
A地 | x | 20 |
B地 | 30 |
(1)设仓库运往A,B两地的总运费为y元.
①将表格补充完整.
②求y关于x的函数表达式.
(2)若仓库运往A地的费用不超过运往A,B两地费用的![]() ,求总运费的最小值.
,求总运费的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ADB、△BCD都是等边三角形,点E,F分别是AB,AD上两个动点,满足AE=DF.连接BF与DE相交于点G,CH⊥BF,垂足为H,连接CG.若DG=![]() ,BG=
,BG=![]() ,且
,且![]() 、
、![]() 满足下列关系:
满足下列关系:![]() ,
,![]() ,则GH= .
,则GH= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com