
【题目】学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个A奖品和2个B奖品共需130元;购买5个A奖品和4个B奖品共需230元.
(1)求A,B两种奖品的单价;
(2)学校准备购买A,B两种奖品共40个,且A奖品的数量不少于B奖品数量的![]() .购买预算金不超过920元,请问学校有几种购买方案.
.购买预算金不超过920元,请问学校有几种购买方案.
【答案】(1)A种奖品的单价为30元,B种奖品的单价为20元.(2)学校有三种购买方案,方案一:购买A种奖品10个,B种奖品30个;方案二:购买A种奖品11个,B种奖品29个;方案三:购买A种奖品12个,B种奖品28个.
【解析】
(1)设A种奖品的单价为x元,B种奖品的单价为y元,根据“购买3个A奖品和2个B奖品共需130元;购买5个A奖品和4个B奖品共需230元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购买A种奖品m个,则购买B种奖品(40﹣m)个,根据购买A种奖品的数量不少于B种奖品数量的![]() 且购买预算金不超过920元,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,再结合m为整数即可得出各购买方案.
且购买预算金不超过920元,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,再结合m为整数即可得出各购买方案.
解:(1)设A种奖品的单价为x元,B种奖品的单价为y元,
依题意,得:![]() ,
,
解得:![]() .
.
答:A种奖品的单价为30元,B种奖品的单价为20元.
(2)设购买A种奖品m个,则购买B种奖品(40﹣m)个,
依题意,得: ,
,
解得:10≤m≤12.
∵m为整数,
∴m=10,11,12,
∴40﹣m=30,29,28.
∴学校有三种购买方案,方案一:购买A种奖品10个,B种奖品30个;方案二:购买A种奖品11个,B种奖品29个;方案三:购买A种奖品12个,B种奖品28个.


科目:初中数学 来源: 题型:
【题目】如图,P是∠AOB的平分线上的一点,PC⊥OA,PD⊥OB,垂足分别为C,D.下列结论 不一定成立的是( )

A.∠AOP=∠BOPB.PC=PD
C.∠OPC=∠OPDD.OP=PC+PD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个n位自然数![]() 能被x0整除,依次轮换个位数字得到的新数
能被x0整除,依次轮换个位数字得到的新数![]() 能被x0+1整除,再依次轮换个位数字得到的新数
能被x0+1整除,再依次轮换个位数字得到的新数![]() 能被x0+2整除,按此规律轮换后,
能被x0+2整除,按此规律轮换后,![]() 能被x0+3整除,…,
能被x0+3整除,…,![]() 能被x0+n﹣1整除,则称这个n位数
能被x0+n﹣1整除,则称这个n位数![]() 是x0的一个“轮换数”.
是x0的一个“轮换数”.
例如:60能被5整除,06能被6整除,则称两位数60是5的一个“轮换数”;
再如:324能被2整除,243能被3整除,432能被4整除,则称三位数324是2个一个“轮换数”.
(1)若一个两位自然数的个位数字是十位数字的2倍,求证这个两位自然数一定是“轮换数”.
(2)若三位自然数![]() 是3的一个“轮换数”,其中a=2,求这个三位自然数
是3的一个“轮换数”,其中a=2,求这个三位自然数![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:一般地,![]() 个相同的因数
个相同的因数![]() 相乘
相乘 ![]() ,记为
,记为![]() .如
.如![]() ,此时,
,此时,![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记为
的对数,记为![]() (即
(即![]() ).一般地,若
).一般地,若![]() ,(
,(![]() 且
且![]() ,
,![]() ),则
),则![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记为
的对数,记为![]() (即
(即![]() ).如
).如![]() ,则
,则![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记为
的对数,记为![]() (即
(即![]() ).
).
(1)计算以下各对数的值:![]() __________,
__________,![]() __________,
__________,![]() __________.
__________.
(2)观察(1)中三数![]() 、
、![]() ,
,![]() 之间满足怎样的关系式,
之间满足怎样的关系式,![]() 、
、![]() 、
、![]() 之间又满足怎样的关系式;
之间又满足怎样的关系式;
(3)由(2)的结果,你能归纳出一个一般性的结论吗?![]() __________.(
__________.(![]() 且
且![]() ,
,![]() ,
,![]() )
)
(4)根据幂的运算法则:![]() 以及对数的含义证明上述结论.
以及对数的含义证明上述结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
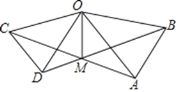
【题目】如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的是____________________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个正整数m能写成m=(a﹣b)(a+b)(a、b均为正整数,且a≠b),则称m为“完美数”,a、b为m的一个完美变形,在m的所有完美变形中,若a2+b2最大,则称a、b为m的最佳完美变形,此时F(m)=a2+b2.例如:12=(4+2)(4﹣2),12为“完美数”,4和2为12的一个完美变形,32=(9+7)(9﹣7)=(6+2)(6﹣2),因为92+72>62+22,所以9和7是32的最佳完美变形,所以F(32)=130.
(1)8 (填“是”或“不是”)完美数;10 (填“是”或“不是”)完美数;13 (填“是”或“不是”)完美数;
(2)求F(48);
(3)若一个两位数n的十位数字和个位数字分别为x,y(1≤x≤y≤9),n为“完美数”且x+y能被8整除,求F(n)的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕着点B顺时针旋转角a(0°<a<90°)得到△A1BC;A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
(1)如图1,观察并猜想,在旋转过程中,线段BE与BF有怎样的数量关系?并证明你的结论.
(2)如图2,当a=30°时,试判断四边形BC1DA的形状,并证明.
(3)在(2)的条件下,求线段DE的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为原点,平行于x轴的直线与抛物线L:y=ax2相交于A,B两点(点B在第一象限),点C在AB的延长线上.
(1)已知a=1,点B的纵坐标为2.如图1,向右平移抛物线L使该抛物线过点B,与AB的延长线交于点C,AC的长为__.
(2)如图2,若BC=AB,过O,B,C三点的抛物线L3,顶点为P,开口向下,对应函数的二次项系数为a3,![]() =__.
=__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地为了鼓励居民节约用水,决定实行两级收费制,即每月用水量不超过14吨(含14吨)时,每吨按政府补贴优惠价收费;每月超过14吨时,超过部分每吨按市场调节价收费,小英家1月份用水20吨,交水费29元;2月份用水18吨,交水费24元.
(1)求每吨水的政府补贴优惠价和市场调节价分别是多少?
(2)小英家3月份用水24吨,她家应交水费多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com