
【题目】在平面直角坐标系中,点O为原点,平行于x轴的直线与抛物线L:y=ax2相交于A,B两点(点B在第一象限),点C在AB的延长线上.
(1)已知a=1,点B的纵坐标为2.如图1,向右平移抛物线L使该抛物线过点B,与AB的延长线交于点C,AC的长为__.
(2)如图2,若BC=AB,过O,B,C三点的抛物线L3,顶点为P,开口向下,对应函数的二次项系数为a3,![]() =__.
=__.

【答案】4![]() ﹣
﹣![]()
【解析】
解:(1)当a=1时,抛物线L的解析式为:y=x2,
当y=2时,2=x2,
∴x=±![]() ,
,
∵B在第一象限,
∴A(﹣![]() ,2),B(
,2),B(![]() ,2),
,2),
∴AB=2![]() ,
,
∵向右平移抛物线L使该抛物线过点B,
∴AB=BC=2![]() ,
,
∴AC=4![]() ;
;
(2)如图2,设抛物线L3与x轴的交点为G,其对称轴与x轴交于Q,过B作BK⊥x轴于K,
设OK=t,则AB=BC=2t,
∴B(t,at2),
根据抛物线的对称性得:OQ=2t,OG=2OQ=4t,
∴O(0,0),G(4t,0),
设抛物线L3的解析式为:y=a3(x﹣0)(x﹣4t),
y=a3x(x﹣4t),
∵该抛物线过点B(t,at2),
∴at2=a3t(t﹣4t),
∵t≠0,
∴a=﹣3a3,
∴![]() =﹣
=﹣![]() ,
,
故答案为:(1)4![]() ;(2)﹣
;(2)﹣![]() .
.



科目:初中数学 来源: 题型:
【题目】已知BC=5,AB=1,AB⊥BC,射线CM⊥BC,动点P在线段BC上(不与点B,C重合),过点P作DP⊥AP交射线CM于点D,连接AD.
(1)如图1,若BP=4,判断△ADP的形状,并加以证明.
(2)如图2,若BP=1,作点C关于直线DP的对称点C′,连接AC′.
①依题意补全图2;
②请直接写出线段AC′的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个A奖品和2个B奖品共需130元;购买5个A奖品和4个B奖品共需230元.
(1)求A,B两种奖品的单价;
(2)学校准备购买A,B两种奖品共40个,且A奖品的数量不少于B奖品数量的![]() .购买预算金不超过920元,请问学校有几种购买方案.
.购买预算金不超过920元,请问学校有几种购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32,连接BD,AE⊥BD,垂足为E.
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从水平地面看一山坡上的通讯铁塔PC,在点A处用测角仪测得塔顶端点P的仰角是45°,向前走9m到达B点,用测角仪测得塔顶端点P和塔底端点C的仰角分别是60°和30°.

(1)求∠BPC的度数.
(2)求该铁塔PF的高度,(结果精确到0.1m,参考数据:![]() ≈1.73.)
≈1.73.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州瓯柑,声名远播.某经销商欲将仓库的120吨瓯柑运往A,B两地销售.运往A,B两地的瓯柑(吨)和每吨的运费如下表.设仓库运往A地的瓯柑为x吨,且x为整数.
瓯柑(吨) | 运费(元/吨) | |
A地 | x | 20 |
B地 | 30 |
(1)设仓库运往A,B两地的总运费为y元.
①将表格补充完整.
②求y关于x的函数表达式.
(2)若仓库运往A地的费用不超过运往A,B两地费用的![]() ,求总运费的最小值.
,求总运费的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
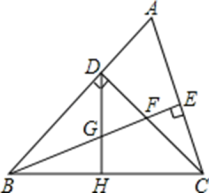
【题目】已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G.
(1)求证:BF=AC;
(2)求证:CE=![]() BF.
BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售![]() ,
,![]() 两种型号的新能源汽车。上周售出1辆
两种型号的新能源汽车。上周售出1辆![]() 型车和3辆
型车和3辆![]() 型车,销售额为96万元,本周已售出2辆
型车,销售额为96万元,本周已售出2辆![]() 型车和1辆
型车和1辆![]() 型车,销售额为62万元。
型车,销售额为62万元。
(1)求每辆![]() 型车和
型车和![]() 型车的售价各为多少?
型车的售价各为多少?
(2)随着汽车限购政策的推行,预计下周起![]() ,
,![]() 两种型号的汽车价格在原有的基础均有上涨,若
两种型号的汽车价格在原有的基础均有上涨,若![]() 型汽车价格上涨m%,
型汽车价格上涨m%,![]() 型汽车价格上涨3m%,则同时购买一台
型汽车价格上涨3m%,则同时购买一台![]() 型车和一台
型车和一台![]() 型车的费用比涨价前多12%,求
型车的费用比涨价前多12%,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=kx(k≠0)沿着y轴向上平移3个单位长度后,与x轴交于点B(3,0),与y轴交于点C,抛物线y=x2+bx+c过点B、C且与x轴的另一个交点为A.
(1)求直线BC及该抛物线的表达式;
(2)设该抛物线的顶点为D,求△DBC的面积;
(3)如果点F在y轴上,且∠CDF=45°,求点F的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com