
【题目】如图,从水平地面看一山坡上的通讯铁塔PC,在点A处用测角仪测得塔顶端点P的仰角是45°,向前走9m到达B点,用测角仪测得塔顶端点P和塔底端点C的仰角分别是60°和30°.

(1)求∠BPC的度数.
(2)求该铁塔PF的高度,(结果精确到0.1m,参考数据:![]() ≈1.73.)
≈1.73.)
【答案】(1)30°;(2)该铁塔PF的高度约为21.3 m
【解析】
试题(1)延长PC交直线AB于点G,根据直角三角形两锐角互余求得即可;
(2)设PE=x米,在直角△APE和直角△BPE中,根据三角函数利用x表示出AE和BE,根据AB=AE﹣BE即可列出方程求得x的值,再在直角△BCE中利用三角函数求得CE的长,则PF的长度即可求解.
试题解析:解:(1)延长PC交直线AB于点F,交直线DE于点G,则PF⊥AF,依题意得:∠PAF=45°,∠PBF=60°,∠CBF=30°,∴∠BPC=90°﹣60°=30°;
(2)根据题意得:AB=DE=9,FG=AD=1.3,设PC=x m,则CB=CP=x.在Rt△CBF中,BF=xcos30°=![]() x,CF=
x,CF=![]() x.在Rt△APF中,FA=FP,∴9+
x.在Rt△APF中,FA=FP,∴9+![]() x=
x=![]() x+x,x=9+3
x+x,x=9+3 ![]() ,∴PC=9+3
,∴PC=9+3 ![]() ≈14.2,∴PF=
≈14.2,∴PF=![]() x+x=21.3.
x+x=21.3.
答:该铁塔PF的高度约为21.3 m.



科目:初中数学 来源: 题型:
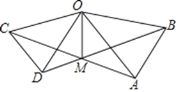
【题目】如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的是____________________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕着点B顺时针旋转角a(0°<a<90°)得到△A1BC;A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
(1)如图1,观察并猜想,在旋转过程中,线段BE与BF有怎样的数量关系?并证明你的结论.
(2)如图2,当a=30°时,试判断四边形BC1DA的形状,并证明.
(3)在(2)的条件下,求线段DE的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知正比例函数![]() 与一次函数
与一次函数![]() 的
的
图像交于点A.
(1)求点A的坐标;
(2)在y轴上确定点M,使得△AOM是等腰三角形,请直接写出点M的坐标;
(3)如图,设x轴上一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交![]() 和
和![]() 的图像于点B、C,连接OC,若BC=
的图像于点B、C,连接OC,若BC=![]() OA,求△ABC的面积及点B、点C的坐标;
OA,求△ABC的面积及点B、点C的坐标;
(4)在(3)的条件下,设直线![]() 交x轴于点D,在直线BC上确定点E,使得△ADE的周长最小,请直接写出点E的坐标.
交x轴于点D,在直线BC上确定点E,使得△ADE的周长最小,请直接写出点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为原点,平行于x轴的直线与抛物线L:y=ax2相交于A,B两点(点B在第一象限),点C在AB的延长线上.
(1)已知a=1,点B的纵坐标为2.如图1,向右平移抛物线L使该抛物线过点B,与AB的延长线交于点C,AC的长为__.
(2)如图2,若BC=AB,过O,B,C三点的抛物线L3,顶点为P,开口向下,对应函数的二次项系数为a3,![]() =__.
=__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.

(1)求证:△ABG≌△C′DG;
(2)求tan∠ABG的值;
(3)求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:≈1.414,≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“创卫工作人人参与,环境卫生人人受益”,我区创卫工作已进入攻坚阶段.某校拟整修学校食堂,现需购买A、B两种型号的防滑地砖共60块,已知A型号地砖每块80元,B型号地砖每块40元.
(1)若采购地砖的费用不超过3200元,那么,最多能购买A型号地砖多少块?
(2)某地砖供应商为了支持创卫工作,现将A、B两种型号的地砖单价都降低a%,这样,该校花费了2560元就购得所需地砖,其中A型号地砖a块,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com