
【题目】如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.

(1)求证:△ABG≌△C′DG;
(2)求tan∠ABG的值;
(3)求EF的长.
【答案】(1)证明见解析(2)7/24(3)25/6
【解析】(1)证明:∵△BDC′由△BDC翻折而成,
∴∠C=∠BAG=90°,C′D=AB=CD,∠AGB=∠DGC′,∴∠ABG=∠ADE。
在△ABG≌△C′DG中,∵∠BAG=∠C,AB= C′D,∠ABG=∠AD C′,
∴△ABG≌△C′DG(ASA)。
(2)解:∵由(1)可知△ABG≌△C′DG,∴GD=GB,∴AG+GB=AD。
设AG=x,则GB=8﹣x,
在Rt△ABG中,∵AB2+AG2=BG2,即62+x2=(8﹣x)2,解得x=![]() 。
。
∴ 。
。
(3)解:∵△AEF是△DEF翻折而成,∴EF垂直平分AD。∴HD=![]() AD=4。
AD=4。
∵tan∠ABG=tan∠ADE=![]() 。∴EH=HD×
。∴EH=HD×![]() =4×
=4×![]() 。
。
∵EF垂直平分AD,AB⊥AD,∴HF是△ABD的中位线。∴HF=![]() AB=
AB=![]() ×6=3。
×6=3。
∴EF=EH+HF=![]() 。
。
(1)根据翻折变换的性质可知∠C=∠BAG=90°,C′D=AB=CD,∠AGB=∠DGC′,故可得出结论。
(2)由(1)可知GD=GB,故AG+GB=AD,设AG=x,则GB=8-x,在Rt△ABG中利用勾股定理即可求出AG的长,从而得出tan∠ABG的值。
(3)由△AEF是△DEF翻折而成可知EF垂直平分AD,故HD=![]() AD=4,再根据tan∠ABG的值即可得出EH的长,同理可得HF是△ABD的中位线,故可得出HF的长,由EF=EH+HF即可得出结果。
AD=4,再根据tan∠ABG的值即可得出EH的长,同理可得HF是△ABD的中位线,故可得出HF的长,由EF=EH+HF即可得出结果。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】(8分)如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.

(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从水平地面看一山坡上的通讯铁塔PC,在点A处用测角仪测得塔顶端点P的仰角是45°,向前走9m到达B点,用测角仪测得塔顶端点P和塔底端点C的仰角分别是60°和30°.

(1)求∠BPC的度数.
(2)求该铁塔PF的高度,(结果精确到0.1m,参考数据:![]() ≈1.73.)
≈1.73.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标第中有一个2×2的正方形网格,每个格点的横、纵坐标均为整数,已知点A(1,2).作直线OA并向右平移k个单位,要使分布在平移后的直线两侧的格点数相同,则k的值为( )
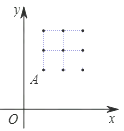
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
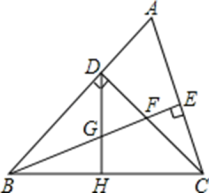
【题目】已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G.
(1)求证:BF=AC;
(2)求证:CE=![]() BF.
BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下:
阅读时间 (小时) | 2 | 2.5 | 3 | 3.5 | 4 |
学生人数(名) | 1 | 2 | 8 | 6 | 3 |
则关于这20名学生阅读小时数的说法正确的是( )
A. 众数是8 B. 中位数是3 C. 平均数是3 D. 方差是0.34
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家出发,外出散步,到一个公共阅报栏前看了一会报后,继续散步了一段时间,然后回家,如图描述了小明在散步过程汇总离家的距离s(米)与散步所用时间t(分)之间的函数关系,根据图象,下列信息错误的是( )

A.小明看报用时8分钟
B.公共阅报栏距小明家200米
C.小明离家最远的距离为400米
D.小明从出发到回家共用时16分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() ,点A、B分别在射线OM、ON上(A、B均不与
,点A、B分别在射线OM、ON上(A、B均不与![]() 重合),以AB为边在∠MON的内部作等边三角形ABC,连接OC.
重合),以AB为边在∠MON的内部作等边三角形ABC,连接OC.
(1)如图1,当OA=OB时,求证:![]() 平分
平分![]() .
.

(2)如图2,当OA≠OB时,过点C作CD⊥OM,CE⊥ON,垂足分别为D、E.求证:OD=OE.(注:四边形的内角和为![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com