练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】将矩形纸片ABCD按如图所示的方式折叠，恰好得到菱形AECF．若AB=6，则菱形AECF的面积为__________.

    【答案】8

    【解析】

    根据菱形AECF，得∠FCO=∠ECO，再利用∠ECO=∠ECB，可通过折叠的性质，结合直角三角形勾股定理求得BC的长，则利用菱形的面积公式即可求解．

    解：∵四边形AECF是菱形，AB=6，
    ∴设BE=x，则AE=6-x，CE=6-x，
    ∵四边形AECF是菱形，∴∠FCO=∠ECO，
    ∵∠ECO=∠ECB，
    ∴∠ECO=∠ECB=∠FCO=30°，2BE=CE，
    ∴CE=2x，∴2x=6-x，解得：x=2，
    ∴CE=AE=4.

    利用勾股定理得出： BC===2，

    ∴菱形的面积=AEBC=8．
    故答案为：8．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，给出以下结论：

    ①因为a＞0，所以函数有最大值；

    ②该函数图象关于直线对称；

    ③当时，函数y的值大于0；

    ④当时，函数y的值都等于0．

    其中正确结论的个数是

    A．1 B．2 C．3 D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠AOB＝60°，点P在边OA上，点M、N在边OB上．

    （1）若∠PNO＝60°，证明△PON是等边三角形；

    （2）若PM＝PN，OP＝12，MN＝2，求OM的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△OAB和△OCD中，OA＝OB，OC＝OD，OA＞OC，∠AOB＝∠COD＝40°，连接AC，BD交于点M，连接OM．下列结论：①AC＝BD；②∠AMB＝40°；③OM平分∠BOC；④MO平分∠BMC．其中正确的是____________________________

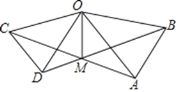
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某生姜种植基地计划种植A,B两种生姜30亩.已知A,B两种生姜的年产量分别为2000千克/亩、2500千克/亩,收购单价分别是8元/千克、7元/千克.

    (1)若该基地收获两种生姜的年总产量为68000千克,求A,B两种生姜各种多少亩?

    (2)若要求种植A种生姜的亩数不少于B种的一半,那么种植A,B两种生姜各多少亩时,全部收购该基地生姜的年总收入最多?最多是多少元?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，AB=BC=2，∠ABC=120°，将△ABC绕着点B顺时针旋转角a（0°＜a＜90°）得到△A1BC；A1B交AC于点E，A1C1分别交AC、BC于D、F两点．

    （1）如图1，观察并猜想，在旋转过程中，线段BE与BF有怎样的数量关系？并证明你的结论．

    （2）如图2，当a=30°时，试判断四边形BC1DA的形状，并证明．

    （3）在（2）的条件下，求线段DE的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，已知正比例函数与一次函数的

    图像交于点A．

    （1）求点A的坐标；

    （2）在y轴上确定点M，使得△AOM是等腰三角形，请直接写出点M的坐标；

    （3）如图，设x轴上一点P（a，0），过点P作x轴的垂线（垂线位于点A的右侧），分别交和的图像于点B、C，连接OC，若BC=OA，求△ABC的面积及点B、点C的坐标；

    （4）在（3）的条件下，设直线交x轴于点D，在直线BC上确定点E，使得△ADE的周长最小，请直接写出点E的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形纸片ABCD中，AB=6，BC=8．把△BCD沿对角线BD折叠，使点C落在C′处，BC′交AD于点G；E、F分别是C′D和BD上的点，线段EF交AD于点H，把△FDE沿EF折叠，使点D落在D′处，点D′恰好与点A重合．

    （1）求证：△ABG≌△C′DG；

    （2）求tan∠ABG的值；

    （3）求EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知：在平面直角坐标系中，每个小正方形的边长为1，△ABC的顶点都在格点上，点A的坐标为（－3，2）.请按要求分别完成下列各小题：

    （1）把△ABC向下平移7个单位，再向右平移7个单位，得到△A1B1C1，画出△A1B1C1；

    （2）画出△A1B1C1关于x轴对称的△A2B2C2；

    画出△A1B1C1关于y轴对称的△A3B3C3；

    （3）求△ABC的面积.

    查看答案和解析>>

    同步练习册答案