
【题目】某生姜种植基地计划种植A,B两种生姜30亩.已知A,B两种生姜的年产量分别为2000千克/亩、2500千克/亩,收购单价分别是8元/千克、7元/千克.
(1)若该基地收获两种生姜的年总产量为68000千克,求A,B两种生姜各种多少亩?
(2)若要求种植A种生姜的亩数不少于B种的一半,那么种植A,B两种生姜各多少亩时,全部收购该基地生姜的年总收入最多?最多是多少元?
【答案】(1)种植A种生姜14亩,种植B种生姜16亩;(2) 种植A种生姜10亩,种植B种生姜20亩时,全部收购该基地生姜的年总收入最多,最多为510000元.
【解析】
试题(1)设该基地种植A种生姜x亩,那么种植B种生姜(30-x)亩,根据:A种生姜的产量+B种生姜的产量=总产量,列方程求解;
(2)设A种生姜x亩,根据A种生姜的亩数不少于B种的一半,列不等式求x的取值范围,再根据(1)的等量关系列出函数关系式,在x的取值范围内求总产量的最大值.
试题解析:(1)设该基地种植A种生姜x亩,那么种植B种生姜(30-x)亩,
根据题意,2000x+2500(30-x)=68000,
解得x=14,
∴30-x=16,
答:种植A种生姜14亩,种植B种生姜16亩;
(2)由题意得,x≥![]() (30-x),解得x≥10,
(30-x),解得x≥10,
设全部收购该基地生姜的年总收入为y元,则
y=8×2000x+7×2500(30-x)=-1500x+525000,
∵y随x的增大而减小,∴当x=10时,y有最大值,
此时,30-x=20,y的最大值为510000元,
答:种植A种生姜10亩,种植B种生姜20亩时,全部收购该基地生姜的年总收入最多,最多为510000元.


 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】珠海到韶关的距离约为360千米,小刘驾驶小轿车,小张驾驶大货车,两人都从珠海去韶关,小刘比小张晚出发90分钟,最后两车同时到达韶关,已知小轿车的速度是大货车速度的1.5倍.
(1)分别求小轿车和大货车的速度;
(2)当小刘行驶了2小时,此时两车相距多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC=12厘米,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为x厘米/秒,则当△BPD与△CQP全等时,x的值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,每个小正方形的边长为1个单位长度.
(1)作出△ABC关于原点对称的△A1B1C1,并写出A1,B1,C1的坐标.
(2)y轴上有一点Q,使AQ+CQ的值最小,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:①OA=OD;②AD⊥EF;③当∠BAC=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.其中正确的是_________.(填序号)
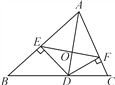
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,□ABCD的对角线AC,BD相交于点O,E、F、G、H分别是OA、OB、OC、OD的中点,那么□ABCD与四边形EFGH是否是位似图形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标第中有一个2×2的正方形网格,每个格点的横、纵坐标均为整数,已知点A(1,2).作直线OA并向右平移k个单位,要使分布在平移后的直线两侧的格点数相同,则k的值为( )
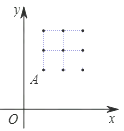
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=2x+a与y=-x+b的图象都经过点A(-2,0)且与y轴分别交于B,C两点

(1)分别求出这两个一次函数的解析式
(2)求△ABC的面积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com