Question

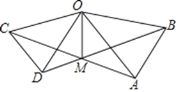
【题目】如图，在△OAB和△OCD中，OA＝OB，OC＝OD，OA＞OC，∠AOB＝∠COD＝40°，连接AC，BD交于点M，连接OM．下列结论：①AC＝BD；②∠AMB＝40°；③OM平分∠BOC；④MO平分∠BMC．其中正确的是____________________________

Answer 1

【答案】①②④

【解析】

由SAS证明△AOC≌△BOD得出∠OCA=∠ODB，AC=BD，①正确；
由全等三角形的性质得出∠OAC=∠OBD，由三角形的外角性质得：∠AMB+∠OAC=∠AOB+∠OBD，得出∠AMB=∠AOB=40°，②正确；
作OG⊥MC于G，OH⊥MB于H，如图2所示：则∠OGC=∠OHD=90°，由AAS证明△OCG≌△ODH（AAS），得出OG=OH，由角平分线的判定方法得出MO平分∠BMC，④正确；
由∠AOB=∠COD，得出当∠DOM=∠AOM时，OM才平分∠BOC，假设∠DOM=∠AOM，由△AOC≌△BOD得出∠COM=∠BOM，由MO平分∠BMC得出∠CMO=∠BMO，推出△COM≌△BOM，得OB=OC，而OA=OB，所以OA=OC，而OA＞OC，故③错误；即可得出结论．

解：∵∠AOB=∠COD=40°，
∴∠AOB+∠AOD=∠COD+∠AOD，
即∠AOC=∠BOD，
在△AOC和△BOD中，

∴△AOC≌△BOD（SAS），
∴∠OCA=∠ODB，AC=BD，①正确；
∴∠OAC=∠OBD，
由三角形的外角性质得：∠AMB+∠OAC=∠AOB+∠OBD，
∴∠AMB=∠AOB=40°，②正确；
作OG⊥MC于G，OH⊥MB于H，如图2所示：

则∠OGC=∠OHD=90°，
在△OCG和△ODH中，

∴△OCG≌△ODH（AAS），
∴OG=OH，
∴MO平分∠BMC，④正确；
∵∠AOB=∠COD，
∴当∠DOM=∠AOM时，OM才平分∠BOC，
假设∠DOM=∠AOM
∵△AOC≌△BOD，
∴∠COM=∠BOM，
∵MO平分∠BMC，
∴∠CMO=∠BMO，
在△COM和△BOM中，

∴△COM≌△BOM（ASA），
∴OB=OC，
∵OA=OB
∴OA=OC
与OA＞OC矛盾，
∴③错误；
正确的是①②④；

故答案为：①②④