Question

【题目】新定义：如图（1）和图（2）中，点P是平面内一点，如果＝2或＝，称点P是线段AB的强弱点．

（1）如图2，在Rt△APB中，∠APB＝90°，∠A＝30°，问：点B是否是线段AP的强弱点？请说明理由；

（2）如图3，在Rt△ABC中，∠ACB＝90°，B是线段AC的强弱点（BA＞BC），BD是Rt△ABC的角平分线，求证：点D是线段AC上的强弱点．

Answer 1

【答案】（1）点B是线段AP的强弱点，理由见解析；（2）见解析

【解析】

（1）在Rt△PAB中，根据直角三角形30度角的性质得：AB和PB的关系，由新定义即可解决问题；

（2）如图3中，由B是线段AC的强弱点（BA＞BC），推出AB＝2BC，可得∠A＝30°，根据角平分线的定义和等腰三角形的判定，直角三角形30度角的性质可得AD＝2CD，解决问题.

（1）解：点B是线段AP的强弱点，理由是：

如图2中，

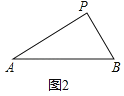
在Rt△PAB中，∠APB＝90°，∠A＝30°，

∴AB＝2PB，

∴＝2，

∴点B是线段AP的强弱点；

（2）证明：如图3中，

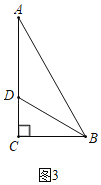
∵B是线段AC的强弱点（BA＞BC），

∴AB＝2BC，

Rt△ACB中，∠A＝30°，∠ABC＝60°，

∵BD平分∠ABC，

∴∠ABD＝∠CBD＝30°＝∠A，

∴AD＝BD，

Rt△BCD中，BD＝2CD，

∴＝2，

∴点D是线段AC上的强弱点．