练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

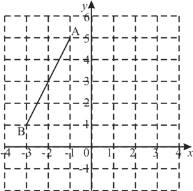
    【题目】如图，在平面直角坐标系中，点A的坐标为（﹣1，5），点B的坐标为（﹣3，1）．

    （1）在平面直角坐标系中作线段AB关于y轴对称的线段A1B1（A与A1，B与B1对应）；

    （2）求△AA1B1的面积；

    （3）在y轴上存在一点P，使PA+PB的值最小，则点P的坐标为________.

    【答案】（1）见解析；（2）4；（3）（0,4）

    【解析】

    （1）利用关于y轴对称的点的坐标特征写出点A1、B1的坐标，然后描点、连线即可；

    （2）根据三角形面积公式计算即可；

    （3）连接AB1交y轴于点P，则点P就是所求的点，根据图形得出坐标即可.

    （1）如图：

    （2）∵A(-1，5)，A1(1，5)，

    ∴AA1=2，

    ∴△AA1B1的面积=；

    （3）连接AB1交y轴于点P，则P(0，4)就是所求的点.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】大双，小双的妈妈申购到一张北京奥运会的门票，兄弟俩决定分别用标有数字且除数字以外没有其它任何区别的小球，各自设计一种游戏确定谁去．

    大双：A袋中放着分别标有数字1，2，3的三个小球，B袋中放着分别标有数字4，5的两个小球，且都已各自搅匀，小双蒙上眼睛从两个口袋中各取出1个小球，若两个小球上的数字之积为偶数，则大双得到门票；若积为奇数，则小双得到门票．

    小双：口袋中放着分别标有数字1，2，3的三个小球，且已搅匀，大双，小双各蒙上眼睛有放回地摸1次，大双摸到偶数就记2分，摸到奇数记0分；小双摸到奇数就记1分，摸到偶数记0分，积分多的就得到门票．（若积分相同，则重复第二次．）

    （1）大双设计的游戏方案对双方是否公平？请你运用列表或树状图说明理由；

    （2）小双设计的游戏方案对双方是否公平？不必说理．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知在四边形ABCD中，点E在AD上，∠BCE=∠ACD=90°，∠BAC=∠D，BC=CE．

    （1）求证：AC=CD；

    （2）若AC=AE，求∠DEC的度数．

    【答案】（1）证明见解析；（2）112.5°．

    【解析】试题分析： 根据同角的余角相等可得到结合条件，再加上 可证得结论；
    根据 得到 根据等腰三角形的性质得到 由平角的定义得到

    试题解析： 证明：

    在△ABC和△DEC中， ，

    （2）∵∠ACD＝90°，AC＝CD，

    ∴∠1＝∠D＝45°，

    ∵AE＝AC，

    ∴∠3＝∠5＝67.5°，

    ∴∠DEC＝180°－∠5＝112.5°．

    【题型】解答题
    【结束】
    21

    【题目】一个零件的形状如图所示，工人师傅按规定做得∠B=90°，

    AB＝3，BC＝4，CD＝12，AD＝13，假如这是一块钢板，你能帮工人师傅计算一下这块钢板的面积吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学举行“庆祝中华人民共和国成立70周年”知识预赛，学生会把成绩（分）分成五组：A组：；B组：；C组：；D组：；E组：.

    统计后绘制成如下两个统计图（不完整）.

    （1）直接填空：

    ①的值为_________；

    ②在图2中，组的扇形圆心角的度数为_________.

    （2）在图1中，画出所对应的条形图；

    （3）若学生会计划从预赛中选拔前30名进入复赛，则进入复赛的成绩应不低于多少分？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，P是∠AOB的平分线上的一点，PC⊥OA，PD⊥OB，垂足分别为C，D.下列结论 不一定成立的是（ ）

    A.∠AOP=∠BOPB.PC=PD

    C.∠OPC=∠OPDD.OP=PC+PD

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在中，，，，根据下列条件不能判断是直角三角形的是（ ）

    A.,B.

    C.，，D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（阅读）例题：在等腰三角形中，若，求的度数.

    点点同学在思考时是这样分析的：，都可能是顶角或底角，因此需要进行分类.他认为画“树状图”可以帮我们不重复，不遗漏地分类（如图），据此可求出的度数.

    （解答）

    由以上思路，可得的度数为__________；

    （应用）

    将一个边长为5，12，13的直角三角形拼上一个三角形后可以拼成一个等腰三角形，图2就是其中的一种拼法.请你利用备用图画出三种可能的情形，使得拼成的等腰三角形腰长为13.

    （注意：请对所拼成图形中的线段长度标注数据）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】兴发服装店老板用4500元购进一批某款T恤衫，由于深受顾客喜爱，很快售完，老板又用4950元购进第二批该款式T恤衫，所购数量与第一批相同，但每件进价比第一批多了9元．

    （1）第一批该款式T恤衫每件进价是多少元？

    （2）老板以每件120元的价格销售该款式T恤衫，当第二批T恤衫售出时，出现了滞销，于是决定降价促销，若要使第二批的销售利润不低于650元，剩余的T恤衫每件售价至少要多少元？（利润=售价﹣进价）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个正整数m能写成m＝（a﹣b）（a+b）（a、b均为正整数，且a≠b），则称m为“完美数”，a、b为m的一个完美变形，在m的所有完美变形中，若a2+b2最大，则称a、b为m的最佳完美变形，此时F（m）＝a2+b2．例如：12＝（4+2）（4﹣2），12为“完美数”，4和2为12的一个完美变形，32＝（9+7）（9﹣7）＝（6+2）（6﹣2），因为92+72＞62+22，所以9和7是32的最佳完美变形，所以F（32）＝130．

    （1）8　 　（填“是”或“不是”）完美数；10　 　（填“是”或“不是”）完美数；13　 　（填“是”或“不是”）完美数；

    （2）求F（48）；

    （3）若一个两位数n的十位数字和个位数字分别为x，y（1≤x≤y≤9），n为“完美数”且x+y能被8整除，求F（n）的最小值．

    查看答案和解析>>

    同步练习册答案