
ЁОЬтФПЁПФГЮФОпЕъРЯАхЕквЛДЮгУ1000дЊЙКНјвЛХњЮФОпЃЌКмПьЯњЪлЭъБЯЃЛЕкЖўДЮЙКНјЪБЗЂЯжУПМўЮФОпНјМлБШЕквЛДЮЩЯеЧСЫ2 5дЊЃЎРЯАхгУ2500дЊЙКНјСЫЕкЖўХњЮФОпЃЌЫљЙКНјЮФОпЕФЪ§СПЪЧЕквЛДЮЙКНјЪ§СПЕФ2БЖЃЌЭЌбљКмПьЯњЪлЭъБЯЃЌСНХњЮФОпЕФЪлМлОљЮЊУПМў15дЊЃЎ
ЃЈ1ЃЉЮЪЕкЖўДЮЙКНјСЫЖрЩйМўЮФОпЃП
ЃЈ2ЃЉЮФОпЕъРЯАхЕквЛДЮЙКНјЕФЮФОпга3% ЕФЫ№КФЃЌЕкЖўДЮЙКНјЕФЮФОпга5% ЕФЫ№КФЃЌЮЪЮФОпЕъРЯАхдкетСНБЪЩњвтжаЪЧгЏРћЛЙЪЧПїБОЃПЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁП(1) 200МўЃЛ(2)гЏРћ805дЊ,РэгЩМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉЩшЕквЛДЮЙКНјxМўЮФОпЃЌдђЕкЖўДЮОЭЙКНј2xМўЃЌИљОнЕкЖўДЮЙКНјЪБЗЂЯжУПМўЮФОпНјМлБШЕквЛДЮЩЯеЧСЫ2 5дЊЃЌЫљЙКНјЮФОпЕФЪ§СПЪЧЕквЛДЮЙКНјЪ§СПЕФ2БЖЃЌПЩСаЗНГЬЧѓНт
ЃЈ2ЃЉРћШѓ=ЪлМл-НјМлЃЌИљОнЃЈ1ЃЉЫуГіМўЪ§ЃЌШЛКѓЫуГізмЪлМлМѕШЅГЩБОМДЮЊЫљЧѓ
НтЃКЃЈ1ЃЉЩшЕквЛДЮЙКНјxМўЮФОпЃЌ
![]()
НтЕУ:x=100
ОМьбщЃЌx=100ЪЧдЗНГЬЕФНт
2x=2ЁС100=200
Д№ЃКЕкЖўДЮЙКНј200МўЮФОп
ЃЈ2ЃЉ[100(1-3%)+200(1-5%)]ЁС15Љ1000Љ2500=805ЃЈдЊЃЉ
Д№ЃКгЏРћ805дЊ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌAB=12ЃЌBC=8ЃЌЙ§ЖдНЧЯпBDжаЕуOЕФжБЯпЗжБ№НЛABЃЌCDБпгкЕуEЃЌFЃЎ

ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮBEDFЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉЕБЫФБпаЮBEDFЪЧСтаЮЪБЃЌЧѓEFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
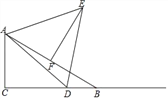
ЁОЬтФПЁПдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌЁЯB=30ЁуЃЌAB=10ЃЌЕуDЪЧЩфЯпCBЩЯЕФвЛИіЖЏЕуЃЌЁїADEЪЧЕШБпШ§НЧаЮЃЌЕуFЪЧABЕФжаЕуЃЌСЌНгEFЃЎ
ЃЈ1ЃЉШчЭМЃЌЕуDдкЯпЖЮCBЩЯЪБЃЌ
ЂйЧѓжЄЃКЁїAEFЁеЁїADCЃЛ
ЂкСЌНгBEЃЌЩшЯпЖЮCD=xЃЌBE=yЃЌЧѓy2Љx2ЕФжЕЃЛ
ЃЈ2ЃЉЕБЁЯDAB=15ЁуЪБЃЌЧѓЁїADEЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдкЦНУцжБНЧзјБъЯЕжагаШ§ЕуAЃЈЉ2ЃЌ1ЃЉЁЂBЃЈ3ЃЌ1ЃЉЁЂCЃЈ2ЃЌ3ЃЉЃЎЧыЛиД№ШчЯТЮЪЬтЃК
ЃЈ1ЃЉдкзјБъЯЕФкУшГіЕуAЁЂBЁЂCЕФЮЛжУЃЌВЂЧѓЁїABCЕФУцЛ§ЃЛ
ЃЈ2ЃЉдкЦНУцжБНЧзјБъЯЕжаЛГіЁїAЁфBЁфCЁфЃЌЪЙЫќгыЁїABCЙигкxжсЖдГЦЃЌВЂаДГіЁїAЁфBЁфCЁфШ§ЖЅЕуЕФзјБъЃЛ
ЃЈ3ЃЉШєMЃЈxЃЌyЃЉЪЧЁїABCФкВПШЮвтвЛЕуЃЌЧыжБНгаДГіетЕудкЁїAЁфBЁфCЁфФкВПЕФЖдгІЕуMЁфЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїADBЁЂЁїBCDЖМЪЧЕШБпШ§НЧаЮЃЌЕуEЃЌFЗжБ№ЪЧABЃЌADЩЯСНИіЖЏЕуЃЌТњзуAE=DFЃЎСЌНгBFгыDEЯрНЛгкЕуGЃЌCHЁЭBFЃЌДЙзуЮЊHЃЌСЌНгCGЃЎШєDG=![]() ЃЌBG=
ЃЌBG=![]() ЃЌЧв
ЃЌЧв![]() ЁЂ
ЁЂ![]() ТњзуЯТСаЙиЯЕЃК
ТњзуЯТСаЙиЯЕЃК![]() ЃЌ
ЃЌ![]() ЃЌдђGH= ЃЎ
ЃЌдђGH= ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉШчЭМЃЈ1ЃЉЃЌвбжЊЃКдкЁїABCжаЃЌЁЯBACЃН90ЁуЃЌAB=ACЃЌжБЯпmОЙ§ЕуAЃЌBDЁЭжБЯпm, CEЁЭжБЯпm,ДЙзуЗжБ№ЮЊЕуDЁЂE.жЄУї:DE=BD+CE.
ЃЈ2ЃЉ ШчЭМЃЈ2ЃЉЃЌНЋЃЈ1ЃЉжаЕФЬѕМўИФЮЊЃКдкЁїABCжаЃЌAB=ACЃЌDЁЂAЁЂEШ§ЕуЖМдкжБЯпmЩЯ,ВЂЧвгаЁЯBDA=ЁЯAEC=ЁЯBAC=![]() ,Цфжа
,Цфжа![]() ЮЊШЮвтШёНЧЛђЖлНЧ.ЧыЮЪНсТлDE=BD+CEЪЧЗёГЩСЂ?ШчГЩСЂ,ЧыФуИјГіжЄУї;ШєВЛГЩСЂ,ЧыЫЕУїРэгЩ.
ЮЊШЮвтШёНЧЛђЖлНЧ.ЧыЮЪНсТлDE=BD+CEЪЧЗёГЩСЂ?ШчГЩСЂ,ЧыФуИјГіжЄУї;ШєВЛГЩСЂ,ЧыЫЕУїРэгЩ.
ЃЈ3ЃЉЭиеЙгыгІгУЃКШчЭМЃЈ3ЃЉЃЌDЁЂEЪЧDЁЂAЁЂEШ§ЕуЫљдкжБЯпmЩЯЕФСНЖЏЕуЃЈDЁЂAЁЂEШ§ЕуЛЅВЛжиКЯЃЉ,ЕуFЮЊЁЯBACЦНЗжЯпЩЯЕФвЛЕу,ЧвЁїABFКЭЁїACFОљЮЊЕШБпШ§НЧаЮЃЌСЌНгBDЁЂCE,ШєЁЯBDA=ЁЯAEC=ЁЯBACЃЌЪдХаЖЯЁїDEFЕФаЮзД.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌЖдНЧЯпACЃЌBDЯрНЛгкЕуOЃЌAB=5ЃЌAC=6ЃЌBD=8ЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮABCDЪЧСтаЮЃЛ
ЃЈ2ЃЉЙ§ЕуAзїAHЁЭBCгкЕуHЃЌЧѓAHЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкШёНЧШ§НЧаЮABCжаЃЌжБЯпlЮЊBCЕФжаДЙЯпЃЌЩфЯпmЮЊЁЯABCЕФНЧЦНЗжЯпЃЌжБЯпlгыmЯрНЛгкЕуP.ШєЁЯBACЃН60ЁуЃЌЁЯACPЃН24ЁуЃЌдђЁЯABPЕФЖШЪ§ЪЧ( )

A. 24Ёу B. 30Ёу C. 32Ёу D. 36Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌЯвCDЁЭABгкЕуGЃЌЕуFЪЧCDЩЯвЛЕуЃЌЧвТњзу![]() =
=![]() ЃЌСЌНгAFВЂбгГЄНЛЁбOгкЕуEЃЌСЌНгADЁЂDEЃЌШєCF=2ЃЌAF=3ЃЎ
ЃЌСЌНгAFВЂбгГЄНЛЁбOгкЕуEЃЌСЌНгADЁЂDEЃЌШєCF=2ЃЌAF=3ЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїADFЁзЁїAEDЃЛ
ЃЈ2ЃЉЧѓFGЕФГЄЃЛ
ЃЈ3ЃЉЧѓжЄЃКtanЁЯE=![]() ЃЎ
ЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com