
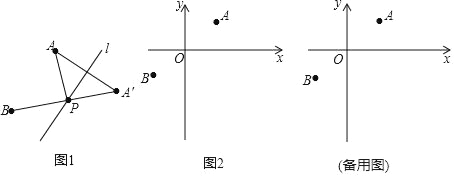
����Ŀ�������壩��ͼ1��A��BΪֱ��lͬ������㣬����A��ֱ��1�ĶԳƵ�A�䣬����A��B��ֱ��l�ڵ�P������AP����Ƶ�PΪ��A��B����ֱ��l�ġ��Ƚǵ㡱��
�����ã���ͼ2����ƽ��ֱ����ϵxOy�У���֪A��2��![]() ����B����2����
����B����2����![]() �����㣮
�����㣮
��1��C��4��![]() ����D��4��
����D��4��![]() ����E��4��
����E��4��![]() �������У����� ���ǵ�A��B����ֱ��x=4�ĵȽǵ㣻
�������У����� ���ǵ�A��B����ֱ��x=4�ĵȽǵ㣻
��2����ֱ��l��ֱ��x�ᣬ��P��m��n���ǵ�A��B����ֱ��l�ĵȽǵ㣬����m��2����APB=������֤��tan![]() =
=![]() ��
��
��3������P�ǵ�A��B����ֱ��y=ax+b��a��0���ĵȽǵ㣬�ҵ�Pλ��ֱ��AB�����·�������APB=60��ʱ����b��ȡֵ��Χ��ֱ��д���������
���𰸡���1��C��2��![]() ��3��b����
��3��b����![]() ��b�٩�2
��b�٩�2![]() ��b��
��b��![]()
��������
��1�������B����ֱ��x=4�ĶԳƵ�B�������꣬����A��B�������ɵ�ֱ��AB��Ľ���ʽ����x=4�������P��������꼴�ɵô𰸣���2����ͼ������A��ֱ��l�ĶԳƵ�A������A��B������ֱ��l�ڵ�P����BH��l�ڵ�H�����ݶԳ��Կ�֪��APG=A��PG���ɡ�AGP=��BHP=90����֤����AGP�ס�BHP���������������ζ�Ӧ�߳ɱ����ɵ�m=![]()
����������ʿ�֪��A=��A��=![]() ����Rt��AGP�У��������ж��弴�ɵý��ۣ���3������Pλ��ֱ��AB�����·�����APB=60��ʱ����P����ABΪ�ң�����Բ��Ϊ60������Բ����AB�·�����ֱ��y=ax+b��a��0����Բ�ཻ����Բ��ֱ��y=ax+b��a��0������һ������ΪQ
����Rt��AGP�У��������ж��弴�ɵý��ۣ���3������Pλ��ֱ��AB�����·�����APB=60��ʱ����P����ABΪ�ң�����Բ��Ϊ60������Բ����AB�·�����ֱ��y=ax+b��a��0����Բ�ཻ����Բ��ֱ��y=ax+b��a��0������һ������ΪQ
���ݶԳ����ʿ�֤����ABQ�ǵȱ������Σ�����QΪ��������ֱ��y=ax+b��a��0����Բ���У���P��Q�غ�������ֱ��y=ax+b��a��0��������Q����OQ������A��Q�ֱ���AM��y�ᣬQN��y�ᣬ����ֱ�ΪM��N����֤����AMO�ס�ONQ���������������ζ�Ӧ�߳ɱ����ɵ�ON��NQ�ij������ɵ�Q�����꣬����A��B��Q����������ֱ��AQ��BQ�Ľ���ʽ������P��A��B�غ�ʱb��ֵ���b��ȡֵ��Χ����.
��1����B����ֱ��x=4�ĶԳƵ�ΪB�䣨10����![]() ����
����
��ֱ��AB������ʽΪ��y=��![]() ��
��
��x=4ʱ��y=![]() ��
��
�ʴ�Ϊ��C
��2����ͼ������A��ֱ��l�ĶԳƵ�A������A��B������ֱ��l�ڵ�P
��BH��l�ڵ�H
�ߵ�A��A������ֱ��l�Գ�
���APG=��A��PG
�ߡ�BPH=��A��PG
���APG=��BPH
�ߡ�AGP=��BHP=90��
���AGP�ס�BHP
��![]() ����
����![]() ��
��
��mn=2![]() ����m=
����m=![]() ��
��
�ߡ�APB=����AP=AP�䣬
���A=��A��=![]() ��
��
��Rt��AGP��tan![]()
![]()
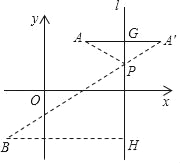
��3����ͼ������Pλ��ֱ��AB�����·�����APB=60��ʱ��
��P����ABΪ�ң�����Բ��Ϊ60������Բ����AB�·�
��ֱ��y=ax+b��a��0����Բ�ཻ����Բ��ֱ��y=ax+b��a��0������һ������ΪQ
�ɶԳ��Կ�֪����APQ=��A��PQ��
�֡�APB=60��
���APQ=��A��PQ=60��
���ABQ=��APQ=60�㣬��AQB=��APB=60��
���BAQ=60��=��AQB=��ABQ
���ABQ�ǵȱ�������
���߶�ABΪ���߶�
���Q����
��ֱ��y=ax+b��a��0����Բ���У���P��Q�غ�
��ֱ��y=ax+b��a��0��������Q
��OQ������A��Q�ֱ���AM��y�ᣬQN��y�ᣬ����ֱ�ΪM��N
��A��2��![]() ����B����2����
����B����2����![]() ��
��
��OA=OB=![]()
�ߡ�ABQ�ǵȱ�������
���AOQ=��BOQ=90�㣬OQ=![]() ��
��
���AOM+��NOD=90��
�֡ߡ�AOM+��MAO=90�㣬��NOQ=��MAO
�ߡ�AMO=��ONQ=90��
���AMO�ס�ONQ
��![]() ,
,
��![]() ��
��
��ON=2![]() ��NQ=3����Q��������3����2
��NQ=3����Q��������3����2![]() ��
��
��ֱ��BQ����ʽΪy=kx+b
��B��Q��������
![]() ��
��
���
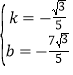 ��
��
��ֱ��BQ�Ľ���ʽΪ��y=��![]() ��
��
��ֱ��AQ�Ľ���ʽΪ��y=mx+n��
��A��Q�������![]() ��
��
���![]() ��
��
��ֱ��AQ�Ľ���ʽΪ��y=��3![]() ��
��
����P��B���غϣ���ֱ��PQ��ֱ��BQ�غϣ���ʱ��b=��![]() ��
��
����P���A�غϣ���ֱ��PQ��ֱ��AQ�غϣ���ʱ��b=![]() ��
��
�֡�y=ax+b��a��0�����ҵ�Pλ��AB���·���
��b����![]() ��b�٩�2
��b�٩�2![]() ��b��
��b��![]() .
.


 ����5��2���ϵ�д�
����5��2���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��![]() ������
������![]() ����
����![]() �ᣬ
�ᣬ![]() ��ֱ���
��ֱ���![]() ��
��![]() ���㣬��
���㣬��![]() ��
��![]()
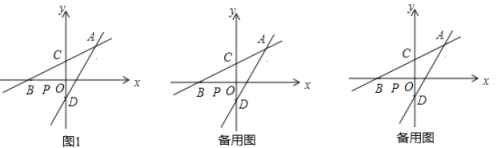
��1����![]() ��ֵ��ֱ��
��ֵ��ֱ��![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2������![]() ����
����![]() �ǵ���������ʱ����
�ǵ���������ʱ����![]() ��ֵ��
��ֵ��
��3����![]() ����
����![]() ��
��![]() �ֱ����߶�
�ֱ����߶�![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() �ǵ���ֱ����������
�ǵ���ֱ����������![]() ʱ����
ʱ����![]() �������______.
�������______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O���ң�AB=2����C��![]() ���˶����ҡ�ACB=30��.
���˶����ҡ�ACB=30��.

��1�����O�İ뾶��
��2�����C��ֱ��AB�ľ���Ϊx��ͼ����Ӱ���ֵ����Ϊy����y��x֮��ĺ�����ϵ����д���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ÿ�����Ľ���ʱ�ڣ���������������������ķ�ʽ��������һ����������������������Ƥ�����������������ȣ�������������ţ�Ϊ�˽����������������������ͬ�����ij����С����������˲��������ʾ�����������ʾ���������ݵ����������������в�������ͳ��ͼ��
��������һһ��ѡ��һ�����ѡ��
A���������������������������ÿ���������
B���������ֽṹ��������������
C��ѡ��������Ʒ�֣����ƹ���ֲ
D���Դ�������ע����������أ������������
E������
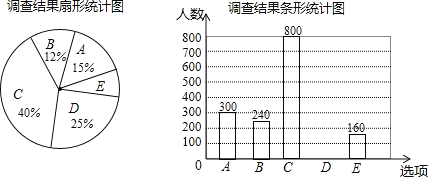
��������ͳ��ͼ������������⣺
��1�����ν��ܵ���������� ���ˣ�
��2������ͳ��ͼ�У�����E��Բ�ĽǶ������� ����
��3���벹ȫ����ͳ��ͼ��
��4��������Լ��90���ˣ��������ͬ��ѡ��������Ʒ�֣����ƹ���ֲ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����MNQ�У�MQ��NQ��
��1��������MNΪһ�ߣ���MN��ͬ���һ������MNQȫ�ȵ������Σ�����ͼ�Σ�����Ҫ˵������ķ�����
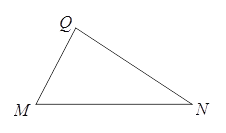
��2���ο���1���й���ȫ�������εķ�������������⣺
��ͼ�����ı���ABCD�У�![]() ����B=��D����֤��CD=AB��
����B=��D����֤��CD=AB��
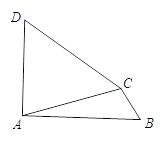
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У���C��40�㣬��B����D��90�㣬E��F�ֱ���BC��DC�ϵ�һ�㣬����AEF���ܳ���Сʱ����EAF�Ķ���Ϊ_____��
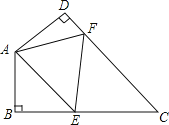
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���![]() �ı���
�ı���![]() �����ǵ������Ϊ
�����ǵ������Ϊ![]() �����ǵĶ�Ӧ�Խ��ߵı�Ϊ________�������ǵ��ܳ�֮��Ϊ
�����ǵĶ�Ӧ�Խ��ߵı�Ϊ________�������ǵ��ܳ�֮��Ϊ![]() �����ı���
�����ı���![]() ���ܳ�Ϊ________��
���ܳ�Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����![]() �ĶԽ����ཻ�ڵ�
�ĶԽ����ཻ�ڵ�![]() ����ô�����������У����ж�
����ô�����������У����ж�![]() Ϊ���ε��ǣ� ��
Ϊ���ε��ǣ� ��
A. ��OAB=��OBA B. ��OAB=��OBC
C. ��OAB=��OCD D. ��OAB=��OAD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AD=![]() AB����BAD��ƽ���߽�BC�ڵ�E��DH��AE�ڵ�H������BH���ӳ���CD�ڵ�F������DE��BF�ڵ�O�����н��ۣ��١�AED=��CED����OE=OD����BH=HF����BC��CF=2HE����AB=HF��������ȷ���У� ��
AB����BAD��ƽ���߽�BC�ڵ�E��DH��AE�ڵ�H������BH���ӳ���CD�ڵ�F������DE��BF�ڵ�O�����н��ۣ��١�AED=��CED����OE=OD����BH=HF����BC��CF=2HE����AB=HF��������ȷ���У� ��

A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com