
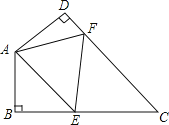
【题目】如图,四边形ABCD中,∠C=40°,∠B=∠D=90°,E、F分别是BC、DC上的一点,当△AEF的周长最小时,∠EAF的度数为_____.
【答案】100°.
【解析】
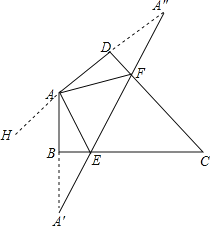
根据要使△AEF的周长最小,即利用点的对称,使三角形的三边在同一直线上,作出A关于BC和CD的对称点A′,A″,即可得出∠AA′E+∠A″=∠HAA′=40°,进而得出∠AEF+∠AFE=2(∠AA′E+∠A″),即可得出答案.
作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于E,交CD于F,
则A′A″即为△AEF的周长最小值.作DA延长线AH,
∵∠C=40°,
∴∠DAB=140°,
∴∠HAA′=40°,
∴∠AA′E+∠A″=∠HAA′=40°,
∵∠EA′A=∠EAA′,∠FAD=∠A″,
∴∠EAA′+∠A″AF=40°,
∴∠EAF=140°﹣40°=100°,
故答案为:100°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
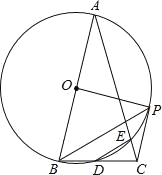
【题目】如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,连结DE,过点B作BP平行于DE,交⊙O于点P,连结EP、CP、OP.
(1)BD=DC吗?说明理由;
(2)求∠BOP的度数;
(3)求证:CP是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校举行一场知识竞赛活动,竞赛共有4小题,每小题5分,答对给5分,答错或不答给0分,在该学校随机抽取若干同学参加比赛,成绩被制成不完整的统计表如下.
成绩 | 人数(频数) | 百分比(频率) |
0 | ||
5 | 0.2 | |
10 | 5 | |
15 | 0.4 | |
20 | 5 | 0.1 |
根据表中已有的信息,下列结论正确的是( )
A. 共有40名同学参加知识竞赛
B. 抽到的同学参加知识竞赛的平均成绩为10分
C. 已知该校共有800名学生,若都参加竞赛,得0分的估计有100人
D. 抽到同学参加知识竞赛成绩的中位数为15分
查看答案和解析>>
科目:初中数学 来源: 题型:
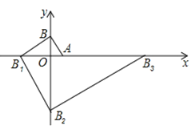
【题目】如图所示,把多块大小不同的![]() 角三角板,摆放在平面直角坐标系中,第一块三角板
角三角板,摆放在平面直角坐标系中,第一块三角板![]() 的一条直角边与
的一条直角边与![]() 轴重合且点
轴重合且点![]() 的坐标为
的坐标为![]() ,
,![]() ,第二块三角板的斜边
,第二块三角板的斜边![]() 与第一块三角板的斜边
与第一块三角板的斜边![]() 垂直且交
垂直且交![]() 轴于点
轴于点![]() ,第三块三角板的斜边
,第三块三角板的斜边![]() 与第二块三角板的斜边
与第二块三角板的斜边![]() 垂直且交
垂直且交![]() 轴于点
轴于点![]() ,第四块三角板斜边
,第四块三角板斜边![]() 与第三块三角板的斜边
与第三块三角板的斜边![]() 垂直且交
垂直且交![]() 轴于点
轴于点![]() ,按此规律继续下去,则点
,按此规律继续下去,则点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
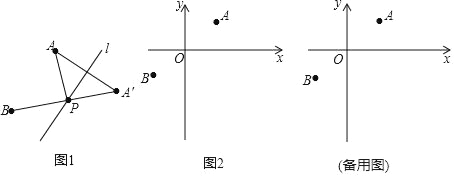
【题目】(定义)如图1,A,B为直线l同侧的两点,过点A作直线1的对称点A′,连接A′B交直线l于点P,连接AP,则称点P为点A,B关于直线l的“等角点”.
(运用)如图2,在平面直坐标系xOy中,已知A(2,![]() ),B(﹣2,﹣
),B(﹣2,﹣![]() )两点.
)两点.
(1)C(4,![]() ),D(4,
),D(4,![]() ),E(4,
),E(4,![]() )三点中,点 是点A,B关于直线x=4的等角点;
)三点中,点 是点A,B关于直线x=4的等角点;
(2)若直线l垂直于x轴,点P(m,n)是点A,B关于直线l的等角点,其中m>2,∠APB=α,求证:tan![]() =
=![]() ;
;
(3)若点P是点A,B关于直线y=ax+b(a≠0)的等角点,且点P位于直线AB的右下方,当∠APB=60°时,求b的取值范围(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A(2,0)的两条直线![]() ,
,![]() 分别交
分别交![]() 轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=
轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=![]() .
.

(1)求点B的坐标;
(2)若△ABC的面积为4,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC,则∠BDF的度数是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6, ![]() .求BE的长.
.求BE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com