
【题目】如图,AB是⊙O的弦,AB=2,点C在![]() 上运动,且∠ACB=30°.
上运动,且∠ACB=30°.

(1)求⊙O的半径;
(2)设点C到直线AB的距离为x,图中阴影部分的面积为y,求y与x之间的函数关系,并写出自变量x的取值范围.
【答案】(1)![]() 的半径是2;(2)
的半径是2;(2)![]() .
.
【解析】试题分析:(1)根据圆周角定理得到△AOB是等边三角形,求出 O的半径;(2)根据图形可得阴影部分面积为三角形ABP的面积+弓形AB的面积,用含有x的代数式表示阴影部分的面积即可,注意x的取值范围.
试题解析:(1)∵∠APB=30°,
∴∠AOB=60°,
∵AO=BO,
∴△AOB是等边三角形,
∵AB=2,
∴OA=OB=2,
∴☉O的半径为2;
(2)过O作OD⊥AB交AB于点C.
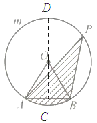
∵OA=OB ,OD⊥AB, AB=2,
∴AC=CB=1,
∴OC=![]() ,
,
∴S△ABP=![]() ·AB·x=x,
·AB·x=x,
S阴影=![]()
![]() ·AB·OC+x,
·AB·OC+x,
计算得S阴影=![]()
![]() +x,
+x,
结合已知可得当x取最大值时,P点的位置在点D处.
此时CD=CO+OP=2+![]() .
.
那么x的取值范围是0≤x<2+![]() ,
,
所以y= x+![]()
![]() (0≤x<2+
(0≤x<2+![]() ).
).


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
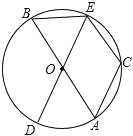
【题目】如图,在⊙O中,AB、DE为⊙O的直径,C是⊙O上一点,且![]() =
=![]() .
.
(1)BE与CE有什么数量关系?为什么?
(2)若∠BOE=60°,则四边形OACE是什么特殊的四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,D是![]() 中点,若∠BAC=70°,求∠C.
中点,若∠BAC=70°,求∠C.
下面是小雯的解法,请帮他补充完整.
解:在⊙O中,
∵D是![]() 的中点
的中点
∴![]() =
=![]() ,
,
∴∠l=∠2( )(填推理的依据)
∵∠BAC=70°
∴∠2=35°
∵AB是⊙O的直径,
∴∠ADB=90°( )(填推理的依据)
∴∠B=90°﹣∠2=55°
∵A、B、C、D四个点都在⊙O上,
∴∠C+∠B=180°( )(填推理的依据)
∴∠C=l80°﹣∠B= (填计算结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2017年3月起,成都市中心城区居民用水实行以户为单位的三级阶梯收费办法:
第I级:居民每户每月用水18吨以内含18吨每吨收水费a元;
第Ⅱ级:居民每户每月用水超过18吨但不超过25吨,未超过18吨的部分按照第Ⅰ级标准收费,超过部分每吨收水费b元;
第Ⅲ级:居民每户每月用水超过25吨,未超过25吨的部分按照第I、Ⅱ级标准收费,超过部分每吨收水费c元.
设一户居民月用水x吨,应缴水费为y元,y与x之间的函数关系如图所示
(1)根据图象直接作答:a= ,b= ;
(2)求当x≥25时y与x之间的函数关系;
(3)把上述水费阶梯收费办法称为方案①,假设还存在方案②:居民每户月用水一律按照每吨4元的标准缴费,请你根据居民每户月“用水量的大小设计出对居民缴费最实惠的方案.(写出过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
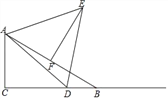
【题目】在Rt△ABC中,∠C=90°,∠B=30°,AB=10,点D是射线CB上的一个动点,△ADE是等边三角形,点F是AB的中点,连接EF.
(1)如图,点D在线段CB上时,
①求证:△AEF≌△ADC;
②连接BE,设线段CD=x,BE=y,求y2﹣x2的值;
(2)当∠DAB=15°时,求△ADE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校举行一场知识竞赛活动,竞赛共有4小题,每小题5分,答对给5分,答错或不答给0分,在该学校随机抽取若干同学参加比赛,成绩被制成不完整的统计表如下.
成绩 | 人数(频数) | 百分比(频率) |
0 | ||
5 | 0.2 | |
10 | 5 | |
15 | 0.4 | |
20 | 5 | 0.1 |
根据表中已有的信息,下列结论正确的是( )
A. 共有40名同学参加知识竞赛
B. 抽到的同学参加知识竞赛的平均成绩为10分
C. 已知该校共有800名学生,若都参加竞赛,得0分的估计有100人
D. 抽到同学参加知识竞赛成绩的中位数为15分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求tan∠BAF的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
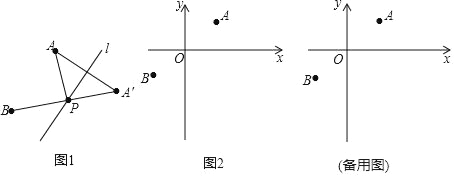
【题目】(定义)如图1,A,B为直线l同侧的两点,过点A作直线1的对称点A′,连接A′B交直线l于点P,连接AP,则称点P为点A,B关于直线l的“等角点”.
(运用)如图2,在平面直坐标系xOy中,已知A(2,![]() ),B(﹣2,﹣
),B(﹣2,﹣![]() )两点.
)两点.
(1)C(4,![]() ),D(4,
),D(4,![]() ),E(4,
),E(4,![]() )三点中,点 是点A,B关于直线x=4的等角点;
)三点中,点 是点A,B关于直线x=4的等角点;
(2)若直线l垂直于x轴,点P(m,n)是点A,B关于直线l的等角点,其中m>2,∠APB=α,求证:tan![]() =
=![]() ;
;
(3)若点P是点A,B关于直线y=ax+b(a≠0)的等角点,且点P位于直线AB的右下方,当∠APB=60°时,求b的取值范围(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个横截面是正方形的长方体平均截成![]() 段后,每段长
段后,每段长![]() 分米,这样表面积就增加了
分米,这样表面积就增加了![]() 平方分米,原来长方体的表面积是________平方分米,体积是________立方分米.
平方分米,原来长方体的表面积是________平方分米,体积是________立方分米.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com