
����Ŀ����2017��3���𣬳ɶ������ij���������ˮʵ���Ի�Ϊ��λ�����������շѰ취��
��I��������ÿ��ÿ����ˮ18�����ں�18��ÿ����ˮ��aԪ��
�ڢ�����ÿ��ÿ����ˮ����18�ֵ�������25�֣�δ����18�ֵIJ��ְ��յڢ��շѣ���������ÿ����ˮ��bԪ��
�ڢ�����ÿ��ÿ����ˮ����25�֣�δ����25�ֵIJ��ְ��յ�I�����շѣ���������ÿ����ˮ��cԪ��
��һ����������ˮx�֣�Ӧ��ˮ��ΪyԪ��y��x֮��ĺ�����ϵ��ͼ��ʾ
��1������ͼ��ֱ������a���� ����b���� ����
��2����x��25ʱy��x֮��ĺ�����ϵ��
��3��������ˮ�ѽ����շѰ취��Ϊ�����٣����軹���ڷ����ڣ�����ÿ������ˮһ�ɰ���ÿ��4Ԫ�ı��ɷѣ�������ݾ���ÿ��������ˮ���Ĵ�С��Ƴ��Ծ���ɷ���ʵ�ݵķ�������д�����̣�

���𰸡���1��3��4����2����x��25ʱ��y��x֮��ĺ�����ϵʽΪy��6x��68����3����x��34ʱ��ѡ��ɷѷ����ٸ�ʵ�ݣ���x��34ʱ��ѡ�����ֽɷѷ���������ͬ����x��34ʱ��ѡ��ɷѷ����ڸ�ʵ��
��������
��1�����ݵ��ۣ��ܼ������������a��b��ֵ�����ʵý⣻
��2���۲캯��ͼ���ҳ�������꣬���ô���ϵ�������������x��25ʱy��x֮��ĺ�����ϵ��
��3�����ܼۣ��������������ҳ�ѡ��ɷѷ������轻ˮ��y��Ԫ������ˮ����x���֣�֮��ĺ�����ϵʽ���ֱ��ҳ���6x��68��4x��6x��68��4x��6x��68��4xʱx��ȡֵ��Χ��x��ֵ����ѡ����õ͵ķ������ɵó����ۣ�
��1��a��54��18��3��
b����82��54������25��18����4��
�ʴ�Ϊ��3��4��
��2���赱x��25ʱ��y��x֮��ĺ�����ϵʽΪy��mx+n��m��0����
����25��82������35��142������y��mx+n���ã�![]() ��
��
��ã�![]() ��
��
�൱x��25ʱ��y��x֮��ĺ�����ϵʽΪy��6x��68��
��3����������ã�ѡ��ɷѷ������轻ˮ��y��Ԫ������ˮ����x���֣�֮��ĺ�����ϵʽΪy��4x��
��6x��68��4xʱ��x��34��
��6x��68��4xʱ��x��34��
��6x��68��4xʱ��x��34��
�൱x��34ʱ��ѡ��ɷѷ����ٸ�ʵ�ݣ���x��34ʱ��ѡ�����ֽɷѷ���������ͬ����x��34ʱ��ѡ��ɷѷ����ڸ�ʵ�ݣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)��֪����A(3��m)��B(2m��4)����A��B��x�������ȣ���B�����꣮
(2)��A�ڵ������ޣ���mΪ��ֵʱ����A(m+2��3m5)��x��ľ���������y������һ�룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������˽�����ë���������ë����е�·��Ϊ�����ߵ�һ���֣���ͼ������O�����Ϸ�1m��P������һ����ë����еĸ߶�y��m����ˮƽ����x��m��֮�����㺯������ʽy=a��x��4��2+h����֪��O��������ˮƽ����Ϊ5m�������ĸ߶�Ϊ1.55m��
��1����a=�� ![]() ʱ������h��ֵ����ͨ�������жϴ����ܷ������
ʱ������h��ֵ����ͨ�������жϴ����ܷ������
��2���������������ë����е����O��ˮƽ����Ϊ7m�������ĸ߶�Ϊ ![]() m��Q��ʱ���ҿ���ɹ�����a��ֵ��
m��Q��ʱ���ҿ���ɹ�����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��C��AB��һ�㣬��ACM����CBN���ǵȱ������Σ�
��1��˵��AN��MB��
��2������ACM�Ƶ�C����ʱ����ת180�㣬ʹA������CB�ϣ������ԭ��ͼ��������Ҫ���ͼ�Σ�
��3���ڣ�2�����õ���ͼ���У����ۡ�AN��BM���Ƿ����������������˵�����ɣ�����������Ҳ��˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
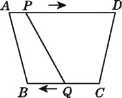
����Ŀ����ͼ,���ı���ABCD��,AD��BC,��AD>BC,BC=6 cm,����P,Q�ֱ��A,Cͬʱ����,P��1 cm/s���ٶ���A��D�˶�,Q��2cm/s���ٶ���C��B�˶�(Q�˶���Bʱ����ͬʱֹͣ�˶�),��________���ı���ABQPΪƽ���ı���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
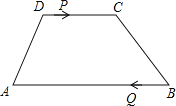
����Ŀ����ͼ������ABCD�У�AB��CD��AB=24cm��DC=10cm����P��Qͬʱ��D��B������P��D��C�˶����ٶ�Ϊÿ��1cm����Q��B��A�˶����ٶ�Ϊÿ��3cm���������P��Q������ABCD�������������γɵ��ı�����ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
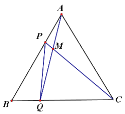
����Ŀ����ͼ����P��Q�ֱ��DZ߳�Ϊ4cm�ĵȱ���ABC��AB��BC�ϵĶ��㣬��P�Ӷ���A����Q�Ӷ���Bͬʱ���������ٶȶ�Ϊ1cm/s������AQ��CP���ڵ�M�������ĸ�����:�١�ABQ�ա�CAP�����ڡ�CMQ�Ķ������䣬ʼ�յ���60���BP��CM����ȷ���м���( )
A. 0 B. 1 C. 2 D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪������A��B�������Ϸֱ��ʾ������a��b����ͼA��B����֮��ľ����ʾΪAB������AB��|a��b|���ش��������⣺
��1�������ϱ�ʾ2��5����֮��ľ������� ���������ϱ�ʾ1�ͩ�3������֮��ľ������� ����
��2����֪|a��3|��7����������a���� ����
��3���������ϱ�ʾ��b�ĵ�λ�ک�4��3������֮�䣬��|b��3|+|b+4|���� ����
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����Rt��ABC��б��BCΪһ���ڡ�ABC��ͬ����������BCEF���������ε�����ΪO������AO�����AB=4��AO=6 ![]() ����ôAC= ��
����ôAC= �� 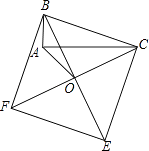
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com