
【题目】如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6 ![]() ,那么AC= .
,那么AC= . 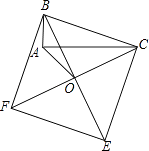
科目:初中数学 来源: 题型:
【题目】自2017年3月起,成都市中心城区居民用水实行以户为单位的三级阶梯收费办法:
第I级:居民每户每月用水18吨以内含18吨每吨收水费a元;
第Ⅱ级:居民每户每月用水超过18吨但不超过25吨,未超过18吨的部分按照第Ⅰ级标准收费,超过部分每吨收水费b元;
第Ⅲ级:居民每户每月用水超过25吨,未超过25吨的部分按照第I、Ⅱ级标准收费,超过部分每吨收水费c元.
设一户居民月用水x吨,应缴水费为y元,y与x之间的函数关系如图所示
(1)根据图象直接作答:a= ,b= ;
(2)求当x≥25时y与x之间的函数关系;
(3)把上述水费阶梯收费办法称为方案①,假设还存在方案②:居民每户月用水一律按照每吨4元的标准缴费,请你根据居民每户月“用水量的大小设计出对居民缴费最实惠的方案.(写出过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店购进一批甲、乙两种款型时尚T恤衫,甲种款型共用了7800元,乙种款型共用了6400元,甲种款型的件数是乙种款型件数的1.5倍,甲种款型每件的进价比乙种款型每件的进价少30元.
(1)甲、乙两种款型的T恤衫各购进多少件?
(2)商店进价提高60%标价销售,销售一段时间后,甲款型全部售完,乙款型剩余一半,商店决定对乙款型按标价的五折降价销售,很快全部售完,求售完 这批T恤衫商店共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国明代珠算家程大位的名著《直指算法统宗》里有一道著名算题:“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,试问大、小和尚各多少人?设大和尚有x人,依题意列方程得( )
A. ![]() +3(100﹣x)=100 B.
+3(100﹣x)=100 B. ![]() ﹣3(100﹣x)=100
﹣3(100﹣x)=100
C. 3x﹣![]() =100 D. 3x+
=100 D. 3x+![]() =100
=100
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A、点B、点C均落在格点上.
(1)S△ABC=;
(2)请在如图所示的网格中,用无刻度的直尺,画出一个以AB为底边的等腰△ABP,使该三角形的面积等于△ABC的面积,并简要说明点P的位置是如何找到的(不要求证明) . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考体育测试前,某区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽取了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图:
请你根据图中的信息,解答下列问题:
(1)写出扇形图中a=%,并补全条形图;
(2)求本次调查获取的样本数据的平均数,众数和中位数;
(3)该区体育中考选报引体向上的男生共有1800人,如果体育中考引体向上达6个以上(含6个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y= ![]() x2+mx+n(n≠0)与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴.
x2+mx+n(n≠0)与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴.
(1)求抛物线的解析式;
(2)设D、E是线段AB上异于A、B的两个动点(点E在点D的上方),DE= ![]() ,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列方程:①![]() ;②0.3x=1;③
;②0.3x=1;③![]() ;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的个数是( )
;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的个数是( )
A. 2B. 3C. 4D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com