
【题目】(1)已知3×9x×81=321,求x的值;
(2)已知am=2,an=5,求①am+n的值;②a3m﹣4n的值.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.
(1)当a=﹣ ![]() 时,①求h的值;②通过计算判断此球能否过网.
时,①求h的值;②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为 ![]() m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且速度都为1cm/s,连接AQ、CP交于点M,下面四个结论:①△ABQ≌△CAP;;②∠CMQ的度数不变,始终等于60°③BP=CM;正确的有几个( )
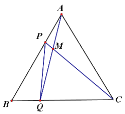
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:点A、B在数轴上分别表示有理数a、b,如图A、B两点之间的距离表示为AB,记作AB=|a﹣b|.回答下列问题:
(1)数轴上表示2和5两点之间的距离是 ,数轴上表示1和﹣3的两点之间的距离是 ;
(2)已知|a﹣3|=7,则有理数a= ;
(3)若数轴上表示数b的点位于﹣4与3的两点之间,则|b﹣3|+|b+4|= .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO︰S△BCO︰S△CAO等于( )

A. 1︰1︰1
B. 1︰2︰3
C. 2︰3︰4
D. 3︰4︰5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是立方体和长方体模型,立方体棱长和长方体底面各边长都为1,长方体侧棱长为2,现用60张长为6宽为4的长方形卡纸,剪出这两种模型的表面展开图,有两种方法:
方法一:如图2,每张卡纸剪出3个立方体表面展开图;
方法二:如图3,每张卡纸剪出2个长方体表面展开图(图中只画出1个).
设用x张卡纸做立方体,其余卡纸做长方体,共做两种模型y个.
(1)在图3中画出第二个长方体表面展开图,用阴影表示;
(2)写出y关于x的函数解析式;
(3)设每只模型(包括立方体和长方体)平均获利为w(元),w满足函数 ![]() ,若想将模型作为教具卖出,且制作的长方体的个数不超过立方体的个数,则应该制作立方体和长方体各多少个,使获得的利润最大?最大利润是多少?
,若想将模型作为教具卖出,且制作的长方体的个数不超过立方体的个数,则应该制作立方体和长方体各多少个,使获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6 ![]() ,那么AC= .
,那么AC= . 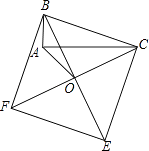
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD绕点A逆时针旋转30°,得到□AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=( )

A.155° B.170° C.105° D.145°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com