
【题目】我们知道:点A、B在数轴上分别表示有理数a、b,如图A、B两点之间的距离表示为AB,记作AB=|a﹣b|.回答下列问题:
(1)数轴上表示2和5两点之间的距离是 ,数轴上表示1和﹣3的两点之间的距离是 ;
(2)已知|a﹣3|=7,则有理数a= ;
(3)若数轴上表示数b的点位于﹣4与3的两点之间,则|b﹣3|+|b+4|= .
![]()
 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE , 求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2017年3月起,成都市中心城区居民用水实行以户为单位的三级阶梯收费办法:
第I级:居民每户每月用水18吨以内含18吨每吨收水费a元;
第Ⅱ级:居民每户每月用水超过18吨但不超过25吨,未超过18吨的部分按照第Ⅰ级标准收费,超过部分每吨收水费b元;
第Ⅲ级:居民每户每月用水超过25吨,未超过25吨的部分按照第I、Ⅱ级标准收费,超过部分每吨收水费c元.
设一户居民月用水x吨,应缴水费为y元,y与x之间的函数关系如图所示
(1)根据图象直接作答:a= ,b= ;
(2)求当x≥25时y与x之间的函数关系;
(3)把上述水费阶梯收费办法称为方案①,假设还存在方案②:居民每户月用水一律按照每吨4元的标准缴费,请你根据居民每户月“用水量的大小设计出对居民缴费最实惠的方案.(写出过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
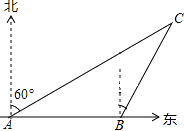
【题目】如图,一渔船自西向东追赶鱼群,在A处测得某无名小岛C在北偏东60°方向上,前进2海里到达B点,此时测得无名小岛C在东北方向上.已知无名小岛周围2.5海里内有暗礁,问渔船继续追赶鱼群有无触礁危险?(参考数据: ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作与思考:一张边长为a的正方形桌面,因为实际需要,需将正方形边长增加b,从而得到一个更大的正方形,木工师傅设计了如图所示的方案:
(1)方案中大正方形的边长都是 ,所以面积为 ;
(2)小明还发现:方案中大正方形的面积还可以用四块小四边形的面积和来表示 ;
(3)你有什么发现,请用数学式子表达 ;
(4)利用(3)的结论计算20.182+2×20.18×19.82+19.822的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数 ![]() (m为常数)的图象与x轴交于点A(﹣3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A,C两点,并与x轴的正半轴交于点B.
(m为常数)的图象与x轴交于点A(﹣3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A,C两点,并与x轴的正半轴交于点B.
(1)求m的值及抛物线的函数表达式;
(2)设E是y轴右侧抛物线上一点,过点E作直线AC的平行线交x轴于点F.是否存在这样的点E,使得以A,C,E,F为顶点的四边形是平行四边形?若存在,求出点E的坐标及相应的平行四边形的面积;若不存在,请说明理由;
(3)若P是抛物线对称轴上使△ACP的周长取得最小值的点,过点P任意作一条与y轴不平行的直线交抛物线于M1(x1 , y1),M2(x2 , y2)两点,试探究 ![]() 是否为定值,并写出探究过程.
是否为定值,并写出探究过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店购进一批甲、乙两种款型时尚T恤衫,甲种款型共用了7800元,乙种款型共用了6400元,甲种款型的件数是乙种款型件数的1.5倍,甲种款型每件的进价比乙种款型每件的进价少30元.
(1)甲、乙两种款型的T恤衫各购进多少件?
(2)商店进价提高60%标价销售,销售一段时间后,甲款型全部售完,乙款型剩余一半,商店决定对乙款型按标价的五折降价销售,很快全部售完,求售完 这批T恤衫商店共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y= ![]() x2+mx+n(n≠0)与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴.
x2+mx+n(n≠0)与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴.
(1)求抛物线的解析式;
(2)设D、E是线段AB上异于A、B的两个动点(点E在点D的上方),DE= ![]() ,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com