
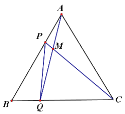
【题目】如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且速度都为1cm/s,连接AQ、CP交于点M,下面四个结论:①△ABQ≌△CAP;;②∠CMQ的度数不变,始终等于60°③BP=CM;正确的有几个( )
A. 0 B. 1 C. 2 D. 3
【答案】C
【解析】
易证△ABQ≌△CAP,可得∠BAQ=∠ACP,即可求得∠AMP=∠BAC=60°,易证∠CQM≠60°,可得CQ≠CM,即可解题.
①∵△ABC是等边三角形,
∴AB=BC=AC,∠BAC=∠B=∠ACB=60°,
根据题意得:AP=BQ,
在△ABQ和△CAP中,
∵AB=AC,∠B=∠CAP,BQ=AP,
∴△ABQ≌△CAP(SAS),①正确;
②∵△ABQ≌△CAP,
∴∠BAQ=∠ACP,
∴∠AMP=∠ACP+∠CAQ=∠BAQ+∠CAQ =∠BAC=60°,
∴∠QMC=60°,②正确;
③∵∠QMC=60°,∠QCM≠60°,
∴∠CQM≠60°,
∴CQ≠CM,
∵BP=CQ,
∴CM≠BP,③错误.
故选C.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上行驶速度不得超过70 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30 m处,过了2 s后,测得小汽车与车速检测仪间距离为50 m,这辆小汽车超速了吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=1,BC= ![]() .将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )
.将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( ) 
A.![]()
B.![]()
C.![]() +1
+1
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2017年3月起,成都市中心城区居民用水实行以户为单位的三级阶梯收费办法:
第I级:居民每户每月用水18吨以内含18吨每吨收水费a元;
第Ⅱ级:居民每户每月用水超过18吨但不超过25吨,未超过18吨的部分按照第Ⅰ级标准收费,超过部分每吨收水费b元;
第Ⅲ级:居民每户每月用水超过25吨,未超过25吨的部分按照第I、Ⅱ级标准收费,超过部分每吨收水费c元.
设一户居民月用水x吨,应缴水费为y元,y与x之间的函数关系如图所示
(1)根据图象直接作答:a= ,b= ;
(2)求当x≥25时y与x之间的函数关系;
(3)把上述水费阶梯收费办法称为方案①,假设还存在方案②:居民每户月用水一律按照每吨4元的标准缴费,请你根据居民每户月“用水量的大小设计出对居民缴费最实惠的方案.(写出过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
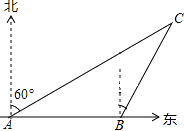
【题目】如图,一渔船自西向东追赶鱼群,在A处测得某无名小岛C在北偏东60°方向上,前进2海里到达B点,此时测得无名小岛C在东北方向上.已知无名小岛周围2.5海里内有暗礁,问渔船继续追赶鱼群有无触礁危险?(参考数据: ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作与思考:一张边长为a的正方形桌面,因为实际需要,需将正方形边长增加b,从而得到一个更大的正方形,木工师傅设计了如图所示的方案:
(1)方案中大正方形的边长都是 ,所以面积为 ;
(2)小明还发现:方案中大正方形的面积还可以用四块小四边形的面积和来表示 ;
(3)你有什么发现,请用数学式子表达 ;
(4)利用(3)的结论计算20.182+2×20.18×19.82+19.822的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考体育测试前,某区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽取了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图:
请你根据图中的信息,解答下列问题:
(1)写出扇形图中a=%,并补全条形图;
(2)求本次调查获取的样本数据的平均数,众数和中位数;
(3)该区体育中考选报引体向上的男生共有1800人,如果体育中考引体向上达6个以上(含6个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com