
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上行驶速度不得超过70 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30 m处,过了2 s后,测得小汽车与车速检测仪间距离为50 m,这辆小汽车超速了吗?

【答案】由题意得AC="30m " AB=50m
∵∠ACB=90°
∴BC=![]()
∴小车行驶速度为40÷2=20米/秒
即为20×3600=72千米/小时
∵72千米/小时>70千米/小时
∴这辆小车超速了。
【解析】
(1)由题意知,△ABC为直角三角形,且AB是斜边,已知AB,AC根据勾股定理可以求BC;
(2)根据BC的长度和时间可以求小汽车在BC路程中的速度,若速度大于70千米/时,则小汽车超速;若速度小于70千米/时,则小汽车没有超速.
解:(1)由题意知,AB=130米,AC=50米,
且在Rt△ABC中,AB是斜边,
根据勾股定理AB2=BC2+AC2,
可以求得:BC=120米=0.12千米,
(2)∵6秒=![]() 小时,
小时,
∴速度为![]() =72千米/小时,
=72千米/小时,
故该小汽车超速.
答:该小汽车超速了,平均速度大于70千米/小时.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
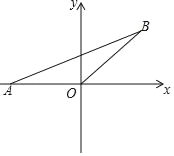
【题目】如图,等腰△AOB中,AO=BO=2,点A在x轴上,OB与x轴的夹角为45°;
(1)求直线AB、OB的解析式;
(2)若将△AOB沿着x轴翻折再向右平移两个单位求直线AB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1= ![]() (x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论:①a=
(x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论:①a= ![]() ;②AC=AE;③△ABD是等腰直角三角形;④当x>1时,y1>y2.其中正确结论的个数是( )
;②AC=AE;③△ABD是等腰直角三角形;④当x>1时,y1>y2.其中正确结论的个数是( )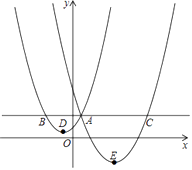
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知两点A(3,m),B(2m,4),且A和B到x轴距离相等,求B点坐标.
(2)点A在第四象限,当m为何值时,点A(m+2,3m5)到x轴的距离是它到y轴距离的一半.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图1,直线l与坐标轴的正半轴分别交于A,B两点,与反比例函数y= ![]() (k>0,x>0)的图象交于C,D两点(点C在点D的左边),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,CE与DF交于点G(a,b).
(k>0,x>0)的图象交于C,D两点(点C在点D的左边),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,CE与DF交于点G(a,b).
(1)若 ![]() ,请用含n的代数式表示
,请用含n的代数式表示 ![]() ;
;
(2)求证:AC=BD;
应用:如图2,直线l与坐标轴的正半轴分别交于点A,B两点,与反比例函数y= ![]() (k>0,x>0)的图象交于点C,D两点(点C在点D的左边),已知
(k>0,x>0)的图象交于点C,D两点(点C在点D的左边),已知 ![]() ,△OBD的面积为1,试用含m的代数式表示k.
,△OBD的面积为1,试用含m的代数式表示k.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一空旷场地上设计一落地为矩形ABCD的小屋,AB+BC=10m,拴住小狗的10m长的绳子一端固定在B点处,小狗在不能进入小屋内的条件下活动,其可以活动的区域面积为S(m2).
(1)如图1,若BC=4m,则S=m2 .
(2)如图2,现考虑在(1)中的矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域,使之变成落地为五边形ABCED的小屋,其他条件不变,则在BC的变化过程中,当S取得最小值时,边BC的长为m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表:
甲 | 乙 | |
进价(元/部) | 4000 | 2500 |
售价(元/部) | 4300 | 3000 |
该商场计划购进两种手机若干部,共需15.5万元,预计全部销售后可获毛利润共2.1万元.
(毛利润=(售价﹣进价)×销售量)
(1)该商场计划购进甲、乙两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.
(1)当a=﹣ ![]() 时,①求h的值;②通过计算判断此球能否过网.
时,①求h的值;②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为 ![]() m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且速度都为1cm/s,连接AQ、CP交于点M,下面四个结论:①△ABQ≌△CAP;;②∠CMQ的度数不变,始终等于60°③BP=CM;正确的有几个( )
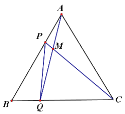
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com