
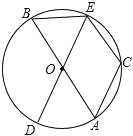
【题目】如图,在⊙O中,AB、DE为⊙O的直径,C是⊙O上一点,且![]() =
=![]() .
.
(1)BE与CE有什么数量关系?为什么?
(2)若∠BOE=60°,则四边形OACE是什么特殊的四边形?请说明理由.
【答案】(1)BE=CE,证明见解析;(2)四边形OACE是菱形,证明见解析;
【解析】
(1)根据对顶角相等得到∠AOD=∠BOE,再根据圆心角、弧、弦的关系得![]() ,加上
,加上![]() ,所以
,所以![]() ,于是有BE=CE;
,于是有BE=CE;
(2)连结OC可得△COE和△AOC是等边三角形,可得四边形OACE的四条边都相等,再根据菱形的判定即可求解.
(1)∵AB、DE是⊙O的直径,
∴∠AOD=∠BOE,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴BE=CE.
(2)连结OC,
∵∠BOE=60°,BE=CE,
∴∠COE=60°,
∵OC=OE,
∴△COE是等边三角形,
∵∠AOC=180°﹣60°﹣60°=60°,OA=OC,
∴△AOC是等边三角形,
∴OE=CE=OA=AC=OC,
∴四边形OACE是菱形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】有甲、乙两个箱子,其中甲箱内有![]() 颗球,分别标记号码
颗球,分别标记号码![]() ,且号码为不重复的整数,乙箱内没有球.已知小育从甲箱内拿出
,且号码为不重复的整数,乙箱内没有球.已知小育从甲箱内拿出![]() 颗球放入乙箱后,乙箱内球的号码的中位数为
颗球放入乙箱后,乙箱内球的号码的中位数为![]() .若此时甲箱内有
.若此时甲箱内有![]() 颗球的号码小于
颗球的号码小于![]() ,有
,有![]() 颗球的号码大于
颗球的号码大于![]() ,若他们的中位数都为
,若他们的中位数都为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 在
在![]() 的
的![]() 边上,
边上,![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,若添加条件________,则四边形
,若添加条件________,则四边形![]() 是矩形;若添加条件________,则四边形
是矩形;若添加条件________,则四边形![]() 是菱形;若添加条件________,则四边形
是菱形;若添加条件________,则四边形![]() 是正方形.
是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA,PB是⊙O的切线,A,B为切点,AC为⊙O的直径,弦BD⊥AC下列结论:①∠P+∠D=180°;②∠COB=∠DAB;③∠DBA=∠ABP;④∠DBO=∠ABP.其中正确的只有( )
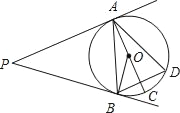
A. ①③ B. ②④ C. ②③ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
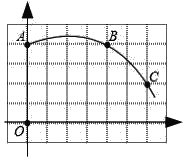
【题目】如图,网格纸中每个小正方形的边长为1,一段圆弧经过格点,点O为坐标原点.
(1)该图中弧所在圆的圆心D的坐标为 ;.
(2)根据(1)中的条件填空:
①圆D的半径= (结果保留根号);
②点(7,0)在圆D (填“上”、“内”或“外”);
③∠ADC的度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司购买了一批![]() 、
、![]() 型芯片,其中
型芯片,其中![]() 型芯片的单价比
型芯片的单价比![]() 型芯片的单价少9元,已知该公司用3120元购买
型芯片的单价少9元,已知该公司用3120元购买![]() 型芯片的条数与用4200元购买
型芯片的条数与用4200元购买![]() 型芯片的条数相等.
型芯片的条数相等.
(1)求该公司购买的![]() 、
、![]() 型芯片的单价各是多少元?
型芯片的单价各是多少元?
(2)若两种芯片共购买了200条,且购买的总费用为6280元,求购买了多少条![]() 型芯片?
型芯片?
查看答案和解析>>
科目:初中数学 来源: 题型:
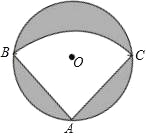
【题目】有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC,如图所示.
(1)求被剪掉阴影部分的面积:
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线![]() 经过点
经过点![]() ,与
,与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,点
两点,点![]() ,
,![]()
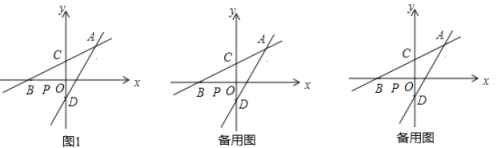
(1)求![]() 的值和直线
的值和直线![]() 的函数表达式;
的函数表达式;
(2)连结![]() ,当
,当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的值;
的值;
(3)若![]() ,点
,点![]() ,
,![]() 分别在线段
分别在线段![]() ,线段
,线段![]() 上,当
上,当![]() 是等腰直角三角形且
是等腰直角三角形且![]() 时,则
时,则![]() 的面积是______.
的面积是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,AB=2,点C在![]() 上运动,且∠ACB=30°.
上运动,且∠ACB=30°.

(1)求⊙O的半径;
(2)设点C到直线AB的距离为x,图中阴影部分的面积为y,求y与x之间的函数关系,并写出自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com