
【题目】有甲、乙两个箱子,其中甲箱内有![]() 颗球,分别标记号码
颗球,分别标记号码![]() ,且号码为不重复的整数,乙箱内没有球.已知小育从甲箱内拿出
,且号码为不重复的整数,乙箱内没有球.已知小育从甲箱内拿出![]() 颗球放入乙箱后,乙箱内球的号码的中位数为
颗球放入乙箱后,乙箱内球的号码的中位数为![]() .若此时甲箱内有
.若此时甲箱内有![]() 颗球的号码小于
颗球的号码小于![]() ,有
,有![]() 颗球的号码大于
颗球的号码大于![]() ,若他们的中位数都为
,若他们的中位数都为![]() ,求
,求![]() 的值.
的值.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某通讯公司推出①,②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分)与费用y(元)之间的函数关系如图所示.
(1)有月租的收费方式是________(填“①”或“②”),月租费是________元;
(2)分别求出①,②两种收费方式中y与自变量x之间的函数表达式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数能表示成两个连续偶数的平方差,那么称这个正整数为“巧数”,如:![]() ,
,![]() ,
,![]() ,因此4,12,20这三个数都是“巧数”.
,因此4,12,20这三个数都是“巧数”.
(1)400和2020这两个数是“巧数”吗?为什么?
(2)设两个连续偶数为![]() 和
和![]() (其中
(其中![]() 取正整数),由这两个连续偶数构造的“巧数”是4的倍数吗?为什么?
取正整数),由这两个连续偶数构造的“巧数”是4的倍数吗?为什么?
(3)求介于50到101之间所有“巧数”之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
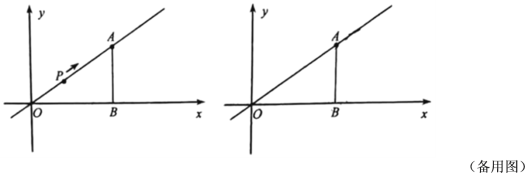
【题目】如图,已知![]() 为正比例函数
为正比例函数![]() 的图像上一点,
的图像上一点,![]() 轴,垂足为点
轴,垂足为点![]() .
.
(1)求![]() 的值;
的值;
(2)点![]() 从
从![]() 出发,以每秒
出发,以每秒![]() 个单位的速度,沿射线
个单位的速度,沿射线![]() 方向运动.设运动时间为
方向运动.设运动时间为![]()
![]() .
.
①过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
②在点![]() 的运动过程中,是否存在这样的
的运动过程中,是否存在这样的![]() ,使得
,使得![]() 为等腰三角形?若存在,请求出所有符合题意的
为等腰三角形?若存在,请求出所有符合题意的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的一元二次方程x2-4x+k+1=0
的一元二次方程x2-4x+k+1=0
(1)若![]() =-1是方程的一个根,求k值和方程的另一根;
=-1是方程的一个根,求k值和方程的另一根;
(2)设x1,x2是关于x的方程x2-4x+k+1=0的两个实数根,是否存在实数k,使得x1x2>x1+x2成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节前夕,某超市用![]() 元购进了一批箱装饮料,上市后很快售完,接着又用
元购进了一批箱装饮料,上市后很快售完,接着又用![]() 元购进第二批这种箱装饮料.已知第二批所购箱装饮料的进价比第一批每箱多
元购进第二批这种箱装饮料.已知第二批所购箱装饮料的进价比第一批每箱多![]() 元,且数量是第一批箱数的
元,且数量是第一批箱数的![]() 倍.
倍.
(1)求第一批箱装饮料每箱的进价是多少元;
(2)若两批箱装饮料按相同的标价出售,为加快销售,商家决定最后的![]() 箱饮料按八折出售,如果两批箱装饮料全部售完利润率不低于
箱饮料按八折出售,如果两批箱装饮料全部售完利润率不低于![]() (不考虑其他因素),那么每箱饮料的标价至少多少元?
(不考虑其他因素),那么每箱饮料的标价至少多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程,乙工程队单独先做10天后,再由甲、乙两个工程队合作20天就能完成全部工作,已知甲工程队单独完成此工程所需天数是乙工程队单独完成此工程所需天数的![]() .
.
(1)求甲、乙工程队单独完成此工程各需多少天;
(2)甲工程队每天的费用为0.67万元,乙工程每天的费用为0.33万元,该工程的预算费用为20万元,若甲、乙工程队一起合作完成该工程,请问工程费用是否够用?若不够用,应追加多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
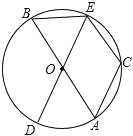
【题目】如图,在⊙O中,AB、DE为⊙O的直径,C是⊙O上一点,且![]() =
=![]() .
.
(1)BE与CE有什么数量关系?为什么?
(2)若∠BOE=60°,则四边形OACE是什么特殊的四边形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com