
【题目】如图,PA,PB是⊙O的切线,A,B为切点,AC为⊙O的直径,弦BD⊥AC下列结论:①∠P+∠D=180°;②∠COB=∠DAB;③∠DBA=∠ABP;④∠DBO=∠ABP.其中正确的只有( )
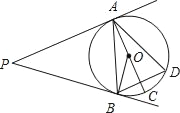
A. ①③ B. ②④ C. ②③ D. ①④
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】某工程,乙工程队单独先做10天后,再由甲、乙两个工程队合作20天就能完成全部工作,已知甲工程队单独完成此工程所需天数是乙工程队单独完成此工程所需天数的![]() .
.
(1)求甲、乙工程队单独完成此工程各需多少天;
(2)甲工程队每天的费用为0.67万元,乙工程每天的费用为0.33万元,该工程的预算费用为20万元,若甲、乙工程队一起合作完成该工程,请问工程费用是否够用?若不够用,应追加多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
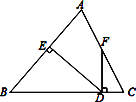
【题目】如图所示,△ABC中,AB=BC,DE⊥AB于点E,DF⊥BC于点D,交AC于F.
⑴若∠AFD=155°,求∠EDF的度数;
⑵若点F是AC的中点,求证:∠CFD=![]() ∠B.
∠B.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以![]() 的边
的边![]() 、
、![]() 为边的等边三角
为边的等边三角![]() 和等边三角形
和等边三角形![]() ,四边形
,四边形![]() 是平行四边形.
是平行四边形.
![]() 当
当![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是矩形;
是矩形;
![]() 当
当![]() 满足什么条件时,平行四边形
满足什么条件时,平行四边形![]() 不存在;
不存在;
![]() 当
当![]() 分别满足什么条件时,平行四边形
分别满足什么条件时,平行四边形![]() 是菱形,正方形?
是菱形,正方形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.

(1)若∠B=70°,求弧CD的度数;
(2)若AB=26,DE=8,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
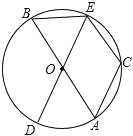
【题目】如图,在⊙O中,AB、DE为⊙O的直径,C是⊙O上一点,且![]() =
=![]() .
.
(1)BE与CE有什么数量关系?为什么?
(2)若∠BOE=60°,则四边形OACE是什么特殊的四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2017年3月起,成都市中心城区居民用水实行以户为单位的三级阶梯收费办法:
第I级:居民每户每月用水18吨以内含18吨每吨收水费a元;
第Ⅱ级:居民每户每月用水超过18吨但不超过25吨,未超过18吨的部分按照第Ⅰ级标准收费,超过部分每吨收水费b元;
第Ⅲ级:居民每户每月用水超过25吨,未超过25吨的部分按照第I、Ⅱ级标准收费,超过部分每吨收水费c元.
设一户居民月用水x吨,应缴水费为y元,y与x之间的函数关系如图所示
(1)根据图象直接作答:a= ,b= ;
(2)求当x≥25时y与x之间的函数关系;
(3)把上述水费阶梯收费办法称为方案①,假设还存在方案②:居民每户月用水一律按照每吨4元的标准缴费,请你根据居民每户月“用水量的大小设计出对居民缴费最实惠的方案.(写出过程)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com