【题目】如果
的对角线相交于点
，那么在下列条件中，能判断
为菱形的是（ ）
A. ∠OAB=∠OBA B. ∠OAB=∠OBC
C. ∠OAB=∠OCD D. ∠OAB=∠OAD
夺冠金卷全能练考系列答案科目：初中数学 来源： 题型：
【题目】自2017年3月起，成都市中心城区居民用水实行以户为单位的三级阶梯收费办法：
第I级：居民每户每月用水18吨以内含18吨每吨收水费a元；
第Ⅱ级：居民每户每月用水超过18吨但不超过25吨，未超过18吨的部分按照第Ⅰ级标准收费，超过部分每吨收水费b元；
第Ⅲ级：居民每户每月用水超过25吨，未超过25吨的部分按照第I、Ⅱ级标准收费，超过部分每吨收水费c元．
设一户居民月用水x吨，应缴水费为y元，y与x之间的函数关系如图所示
（1）根据图象直接作答：a＝ ，b＝ ；
（2）求当x≥25时y与x之间的函数关系；
（3）把上述水费阶梯收费办法称为方案①，假设还存在方案②：居民每户月用水一律按照每吨4元的标准缴费，请你根据居民每户月“用水量的大小设计出对居民缴费最实惠的方案．（写出过程）
查看答案和解析>>
科目：初中数学 来源： 题型：
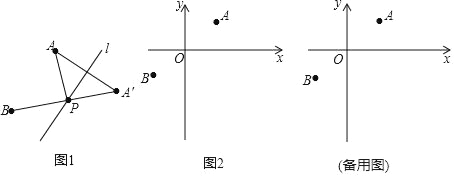
【题目】（定义）如图1，A，B为直线l同侧的两点，过点A作直线1的对称点A′，连接A′B交直线l于点P，连接AP，则称点P为点A，B关于直线l的“等角点”．
（运用）如图2，在平面直坐标系xOy中，已知A（2，
），B（﹣2，﹣）两点．
（1）C（4，
），D（4，
），E（4，
）三点中，点 是点A，B关于直线x=4的等角点；
（2）若直线l垂直于x轴，点P（m，n）是点A，B关于直线l的等角点，其中m＞2，∠APB=α，求证：tan
=
；
（3）若点P是点A，B关于直线y=ax+b（a≠0）的等角点，且点P位于直线AB的右下方，当∠APB=60°时，求b的取值范围（直接写出结果）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，过点A（2，0）的两条直线
，
分别交轴于B，C，其中点B在原点上方，点C在原点下方，已知AB=
.
（1）求点B的坐标；
（2）若△ABC的面积为4，求的解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在南开中学校庆78周年之际，由学生处和美术教研组共同策划、组织了“南开中学校园明信片设计大赛”。获得此次设计大赛组织一等奖的
、
、
、
四个班级一共有75件作品获奖，已知班参赛作品的获奖率为30%，班参赛作品的获奖率为40%。请结合两幅统计图所提供的信息，解决下列问题：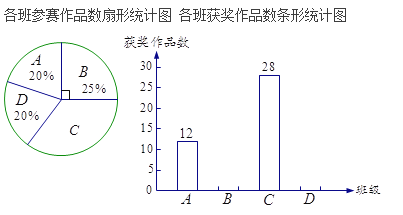
（1）四个班级一共选送了多少件作品参赛，获奖率最高的班级是哪个班；
（2）请将条形统计图补充完整；
（3）班的小欣和小怡同学在本次大赛中荣获个人一等奖，此外、两班各有一名同学荣获个人一等奖。南开中学校友会准备从这4名同学的作品中任选两件，制作成新年贺卡送给老校友。请用列表法或画树状图的方法求出这两件作品分别来自不同班级，且其中一件是小欣或小怡作品的概率.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD中，对角线AC、BD相交于点O，AO=CO，BO=DO，且∠ABC+∠ADC=180°．
（1）求证：四边形ABCD是矩形．
（2）若∠ADF：∠FDC=3：2，DF⊥AC，则∠BDF的度数是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将一个横截面是正方形的长方体平均截成
段后，每段长分米，这样表面积就增加了
平方分米，原来长方体的表面积是________平方分米，体积是________立方分米．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图, 
OAB与
ODC是位似图形 。
试问:(1)AB与CD平行吗？请说明理由 。
(2)如果OB=3,OC=4,OD=3.5.试求
OAB与
ODC的相似比及OA的长 。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，BC=6
，AB=AC，E，F分别为AB，AC上的点（E，F不与A重合），且EF∥BC．将△AEF沿着直线EF向下翻折，得到△A′EF，再展开．
（1）请判断四边形AEA′F的形状，并说明理由；
（2）当四边形AEA′F是正方形，且面积是△ABC的一半时，求AE的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
