
【题目】如图,在△ABC中,BC=6![]() ,AB=AC,E,F分别为AB,AC上的点(E,F不与A重合),且EF∥BC.将△AEF沿着直线EF向下翻折,得到△A′EF,再展开.
,AB=AC,E,F分别为AB,AC上的点(E,F不与A重合),且EF∥BC.将△AEF沿着直线EF向下翻折,得到△A′EF,再展开.
(1)请判断四边形AEA′F的形状,并说明理由;
(2)当四边形AEA′F是正方形,且面积是△ABC的一半时,求AE的长.

【答案】(1)四边形AEA′F为菱形.理由见解析;(2)3.
【解析】
(1)先证明AE=AF,再根据折叠的性质得AE=A′E,AF=A′F,然后根据菱形的判定方法可判断四边形AEA′F为菱形;(2)四先利用四边形AEA′F是正方形得到∠A=90°,则AB=AC=![]() BC=6,然后利用正方形AEA′F的面积是△ABC的一半得到AE2=
BC=6,然后利用正方形AEA′F的面积是△ABC的一半得到AE2=![]()
![]() 66,然后利用算术平方根的定义求AE即可.
66,然后利用算术平方根的定义求AE即可.
(1)四边形AEA′F为菱形.
理由如下:
∵AB=AC,
∴∠B=∠C,
∵EF∥BC,
∴∠AEF=∠B,∠AFE=∠C,
∴∠AEF=∠AFE,
∴AE=AF,
∵△AEF沿着直线EF向下翻折,得到△A′EF,
∴AE=A′E,AF=A′F,
∴AE=A′E=AF=A′F,
∴四边形AEA′F为菱形;
(2)∵四边形AEA′F是正方形,
∴∠A=90°,
∴△ABC为等腰直角三角形,
∴AB=AC=![]() BC=
BC=![]() ×6
×6![]() =6,
=6,
∵正方形AEA′F的面积是△ABC的一半,
∴AE2=![]()
![]() 66,
66,
∴AE=3.


科目:初中数学 来源: 题型:
【题目】如果![]() 的对角线相交于点
的对角线相交于点![]() ,那么在下列条件中,能判断
,那么在下列条件中,能判断![]() 为菱形的是( )
为菱形的是( )
A. ∠OAB=∠OBA B. ∠OAB=∠OBC
C. ∠OAB=∠OCD D. ∠OAB=∠OAD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有( )
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,圆M经过原点O,直线![]() 与x轴、y轴分别相交于A,B两点.
与x轴、y轴分别相交于A,B两点.
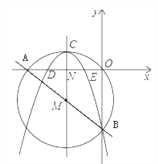
(1)求出A,B两点的坐标;
(2)若有一抛物线的对称轴平行于y轴且经过点M,顶点C在圆M上,开口向下,且经过点B,求此抛物线的函数解析式;
(3)设(2)中的抛物线交![]() 轴于D、E两点,在抛物线上是否存在点P,使得S△PDE=
轴于D、E两点,在抛物线上是否存在点P,使得S△PDE=![]() S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着春节临近,某儿童游乐场推出了甲、乙两种消费卡,设消费次数为![]() 时,所需费用为
时,所需费用为![]() 元,且
元,且![]() 与
与![]() 的函数关系如图所示. 根据图中信息,解答下列问题;
的函数关系如图所示. 根据图中信息,解答下列问题;
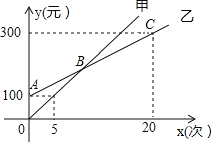
(1)分别求出选择这两种卡消费时,![]() 关于
关于![]() 的函数表达式.
的函数表达式.
(2)求出![]() 点坐标.
点坐标.
(3)洋洋爸爸准备![]() 元钱用于洋洋在该游乐场消费,请问选择哪种消费卡划算?
元钱用于洋洋在该游乐场消费,请问选择哪种消费卡划算?
查看答案和解析>>
科目:初中数学 来源: 题型:
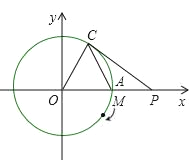
【题目】如图,以O为圆心,4为半径的圆与x轴交于点A,C在⊙O上,∠OAC=60°.
(1)求∠AOC的度数;
(2)P为x轴正半轴上一点,且PA=OA,连接PC,试判断PC与⊙O的位置关系,并说明理由;
(3)有一动点M从A点出发,在⊙O上按顺时针方向运动一周,当S△MAO=S△CAO时,求动点M所经过的弧长,并写出此时M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
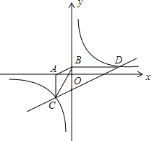
【题目】如图,已知双曲线![]() 经过点
经过点![]() ,点
,点![]() 是双曲线第三象限分支上的动点,过点
是双曲线第三象限分支上的动点,过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴,垂足分别为
轴,垂足分别为![]() ,
,![]() ,连接
,连接![]() ,
,![]() .
.
![]() 求
求![]() 的值;
的值;
![]() 若
若![]() 的面积为
的面积为![]() ,
,
①若直线![]() 的解析式为
的解析式为![]() ,求
,求![]() 、
、![]() 的值;
的值;
②根据图象,直接写出![]() 时
时![]() 的取值范围;
的取值范围;
③判断直线![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,规定把一个三角形先沿x轴翻折,再向右平移两个单位称为一次变换,如图,已知等边三角形ABC的顶点B、C的坐标分别是,(-1,-1),(-3,-1),把三角形ABC经过连续9次这样的变换得到三角形A’B’C’,则点A的对应点A’的坐标是_____
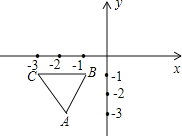
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() ,与
,与![]() 轴交于
轴交于![]() 点,且与
点,且与![]() 轴交点的横坐标分别为
轴交点的横坐标分别为![]() 、
、![]() ,其中
,其中![]() ,
,![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的有( )
.其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com