
【题目】在平面直角坐标系中,规定把一个三角形先沿x轴翻折,再向右平移两个单位称为一次变换,如图,已知等边三角形ABC的顶点B、C的坐标分别是,(-1,-1),(-3,-1),把三角形ABC经过连续9次这样的变换得到三角形A’B’C’,则点A的对应点A’的坐标是_____
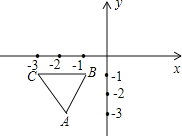
【答案】(16,![]() ).
).
【解析】
首先由△ABC是等边三角形,点B、C的坐标分别是(-1,-1)、(-3,-1),求得点A的坐标,然后根据题意求得第1次、2次、3次变换后的点A的对应点的坐标,即可得规律:第n次变换后的点A的对应点的为:当n为奇数时为(2n-2,1+![]() ),当n为偶数时为(2n-2,-1-
),当n为偶数时为(2n-2,-1-![]() ),继而求得把△ABC经过连续9次这样的变换得到△A′B′C′,则点A的对应点A′的坐标.
),继而求得把△ABC经过连续9次这样的变换得到△A′B′C′,则点A的对应点A′的坐标.
∵△ABC是等边三角形,点B、C的坐标分别是(-1,-1)、(-3,-1),
∴点A的坐标为(-2,-1-![]() ),
),
根据题意得:第1次变换后的点A的对应点的坐标为(-2+2,1+![]() ),即(0,1+
),即(0,1+![]() ),
),
第2次变换后的点A的对应点的坐标为(0+2,-1-![]() ),即(2,-1-
),即(2,-1-![]() ),
),
第3次变换后的点A的对应点的坐标为(2+2,1+![]() ),即(4,1+
),即(4,1+![]() ),
),
第n次变换后的点A的对应点的为:当n为奇数时为(2n-2,1+![]() ),当n为偶数时为(2n-2,-1-
),当n为偶数时为(2n-2,-1-![]() ),
),
∴把△ABC经过连续9次这样的变换得到△A′B′C′,则点A的对应点A′的坐标是:(16,1+![]() ).
).
故答案为:(16,1+![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图, ![]() OAB与
OAB与![]() ODC是位似图形 。
ODC是位似图形 。
试问:(1)AB与CD平行吗?请说明理由 。
(2)如果OB=3,OC=4,OD=3.5.试求![]() OAB与
OAB与![]() ODC的相似比及OA的长 。
ODC的相似比及OA的长 。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC=6![]() ,AB=AC,E,F分别为AB,AC上的点(E,F不与A重合),且EF∥BC.将△AEF沿着直线EF向下翻折,得到△A′EF,再展开.
,AB=AC,E,F分别为AB,AC上的点(E,F不与A重合),且EF∥BC.将△AEF沿着直线EF向下翻折,得到△A′EF,再展开.
(1)请判断四边形AEA′F的形状,并说明理由;
(2)当四边形AEA′F是正方形,且面积是△ABC的一半时,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼![]() (可以看作不透明的长方体)的四周都是空旷的水平地面.地面上有甲、乙两人,他们现在分别位于点
(可以看作不透明的长方体)的四周都是空旷的水平地面.地面上有甲、乙两人,他们现在分别位于点![]() 和点
和点![]() 处,
处,![]() 、
、![]() 均在
均在![]() 的中垂线上,且
的中垂线上,且![]() 、
、![]() 到大楼的距离分别为
到大楼的距离分别为![]() 米和
米和![]() 米,又已知
米,又已知![]() 长
长![]() 米,
米,![]() 长
长![]() 米,由于大楼遮挡着,所以乙不能看到甲.若乙沿着大楼的外面地带行走,直到看到甲(甲保持不动),则他行走的最短距离长为________米.
米,由于大楼遮挡着,所以乙不能看到甲.若乙沿着大楼的外面地带行走,直到看到甲(甲保持不动),则他行走的最短距离长为________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
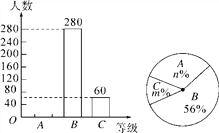
【题目】某报社为了解市民对“社会主义核心价值观”的知晓程度,采取随机抽样的方式进行问卷调查,调查结果分为“A.非常了解”、“B.了解”、“C.基本了解”三个等级,并根据调查结果绘制了如下两幅不完整的统计图.
(1)这次调查的市民人数为________人,m=________,n=________;
(2)补全条形统计图;
(3)若该市约有市民100000人,请你根据抽样调查的结果,估计该市大约有多少人对“社会主义核心价值观”达到“A.非常了解”的程度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把半径为![]() 的圆周按
的圆周按![]() 分割为三段.则最短的弧所对的圆心角为________,该弧和半径围成的扇形的面积为________,最长的弧所对的圆周角为________,最长的弧长是________.
分割为三段.则最短的弧所对的圆心角为________,该弧和半径围成的扇形的面积为________,最长的弧所对的圆周角为________,最长的弧长是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过网格点A(0,4)、B(-4,4)、C(-6,2),请在网格图中进行如下操作:
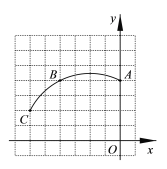
(1)利用网格图确定该圆弧所在圆的圆心D的位置(保留画图痕迹);
(2)连接AD、CD,则⊙D的半径为_ __(结果保留根号),∠ADC的度数为_ __;
(3)若扇形DAC是一个圆锥的侧面展开图,求该圆锥底面半径.(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
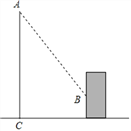
【题目】小左同学想利用影长测量学校旗杆的高度,如图,她在某一时刻立一长度为1米的标杆,测得其影长为![]() 米,同时旗杆投影的一部分在地上,另一部分在某一建筑物的墙上,测得旗杆与建筑物的距离为10米,旗杆在墙上的影高为2米,请帮小左同学算出学校旗杆的高度.
米,同时旗杆投影的一部分在地上,另一部分在某一建筑物的墙上,测得旗杆与建筑物的距离为10米,旗杆在墙上的影高为2米,请帮小左同学算出学校旗杆的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com