
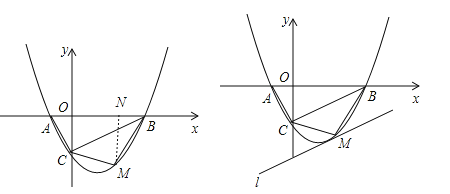
【题目】如图,抛物线![]() (a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.

【答案】(1)![]() ;(2)(
;(2)(![]() ,0);(3)4,M(2,﹣3).
,0);(3)4,M(2,﹣3).
【解析】试题分析:方法一:
(1)该函数解析式只有一个待定系数,只需将B点坐标代入解析式中即可.
(2)首先根据抛物线的解析式确定A点坐标,然后通过证明△ABC是直角三角形来推导出直径AB和圆心的位置,由此确定圆心坐标.
(3)△MBC的面积可由S△MBC=![]() BC×h表示,若要它的面积最大,需要使h取最大值,即点M到直线BC的距离最大,若设一条平行于BC的直线,那么当该直线与抛物线有且只有一个交点时,该交点就是点M.
BC×h表示,若要它的面积最大,需要使h取最大值,即点M到直线BC的距离最大,若设一条平行于BC的直线,那么当该直线与抛物线有且只有一个交点时,该交点就是点M.
方法二:
(1)该函数解析式只有一个待定系数,只需将B点坐标代入解析式中即可.
(2)通过求出A,B,C三点坐标,利用勾股定理或利用斜率垂直公式可求出AC⊥BC,从而求出圆心坐标.
(3)利用三角形面积公式,过M点作x轴垂线,水平底与铅垂高乘积的一半,得出△MBC的面积函数,从而求出M点.
试题解析:解:方法一:
(1)将B(4,0)代入抛物线的解析式中,得: 0=16a﹣![]() ×4﹣2,即:a=
×4﹣2,即:a=![]() ,∴抛物线的解析式为:
,∴抛物线的解析式为: ![]() .
.
(2)由(1)的函数解析式可求得:A(﹣1,0)、C(0,﹣2);
∴OA=1,OC=2,OB=4,即:OC2=OAOB,又:OC⊥AB,∴△OAC∽△OCB,得:∠OCA=∠OBC;
∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°,∴△ABC为直角三角形,AB为△ABC外接圆的直径;
所以该外接圆的圆心为AB的中点,且坐标为:(![]() ,0).
,0).
(3)已求得:B(4,0)、C(0,﹣2),可得直线BC的解析式为:y=![]() x﹣2;
x﹣2;
设直线l∥BC,则该直线的解析式可表示为:y=![]() x+b,当直线l与抛物线只有一个交点时,可列方程:
x+b,当直线l与抛物线只有一个交点时,可列方程:
![]() x+b=
x+b=![]() ,即:
,即: ![]() ,且△=0;
,且△=0;
∴4﹣4×![]() (﹣2﹣b)=0,即b=﹣4;
(﹣2﹣b)=0,即b=﹣4;
∴直线l:y=![]() x﹣4.
x﹣4.
所以点M即直线l和抛物线的唯一交点,有: 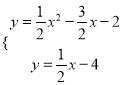 ,解得:
,解得: ![]()
即 M(2,﹣3).
过M点作MN⊥x轴于N,S△BMC=S梯形OCMN+S△MNB﹣S△OCB=![]() ×2×(2+3)+
×2×(2+3)+![]() ×2×3﹣
×2×3﹣![]() ×2×4=4.
×2×4=4.
方法二:
(1)将B(4,0)代入抛物线的解析式中,得: 0=16a﹣![]() ×4﹣2,即:a=
×4﹣2,即:a=![]() ,∴抛物线的解析式为:
,∴抛物线的解析式为: ![]() .
.
(2)∵y=![]() (x﹣4)(x+1),∴A(﹣1,0),B(4,0).C(0,﹣2),∴KAC=
(x﹣4)(x+1),∴A(﹣1,0),B(4,0).C(0,﹣2),∴KAC=![]() =﹣2,KBC=
=﹣2,KBC=![]() =
=![]() ,∴KAC×KBC=﹣1,∴AC⊥BC,∴△ABC是以AB为斜边的直角三角形,△ABC的外接圆的圆心是AB的中点,△ABC的外接圆的圆心坐标为(
,∴KAC×KBC=﹣1,∴AC⊥BC,∴△ABC是以AB为斜边的直角三角形,△ABC的外接圆的圆心是AB的中点,△ABC的外接圆的圆心坐标为(![]() ,0).
,0).
(3)过点M作x轴的垂线交BC′于H,∵B(4,0),C(0,﹣2),∴lBC:y=![]() x﹣2,设H(t,
x﹣2,设H(t, ![]() t﹣2),M(t,
t﹣2),M(t, ![]() ),∴S△MBC=
),∴S△MBC=![]() ×(HY﹣MY)(BX﹣CX)=
×(HY﹣MY)(BX﹣CX)=![]() ×(
×(![]() t﹣2﹣
t﹣2﹣![]() )(4﹣0)=﹣t2+4t,∴当t=2时,S有最大值4,∴M(2,﹣3).
)(4﹣0)=﹣t2+4t,∴当t=2时,S有最大值4,∴M(2,﹣3).
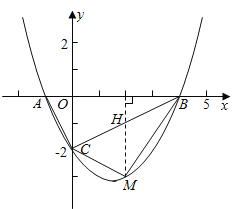
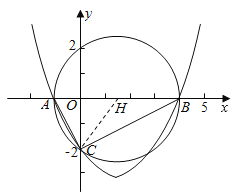


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列四幅图象近似刻画两个变量之间的关系,请按图象顺序将下面四种情景与之对应排序( )

①一辆汽车在公路上匀速行驶(汽车行驶的路程与时间的关系)
②向锥形瓶中匀速注水(水面的高度与注水时间的关系)
③将常温下的温度计插入一杯热水中(温度计的读数与时间的关系)
④一杯越来越凉的水(水温与时间的关系)
A. ③②④①B. ③④②①C. ①④②③D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把自然数按如图的次序排列在直角坐标系中,每个点坐标就对应着一个自然数,例如点(0,0)对应的自然数是1,点(1,2)对应的自然数是14,那么点(1,4)对应的自然数是____;点(n,n)对应的自然数是____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地某月1~20日中午12时的气温(单位:℃)如下:
22 31 25 15 18 23 21 20 27 17 20 12 18 21 21 16 20 24 26 19
(1)将下列频数分布表补充完整:
气温分组 | 划记 | 频数 |
12≤x<17 |
| 3 |
17≤x<22 |
| 10 |
22≤x<27 |
| 5 |
27≤x<32 |
| 2 |

(2)补全频数分布直方图;
(3)根据频数分布表或频数分布直方图,分析数据的分布情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm.动点P、Q分别从点A、B同时开始移动,点P的速度为1 cm/秒,点Q的速度为2 cm/秒,点Q移动到点C后停止,点P也随之停止运动下列时间瞬间中,能使△PBQ的面积为15cm 的是( )
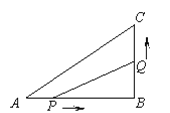
A. 2秒钟 B. 3秒钟 C. 4秒钟 D. 5秒钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△P1OA1,△P2A1A2,△P3A2A3,…都是等腰直角三角形,其直角顶点P1(3,3),P2,P3,…均在直线y=﹣![]() x+4上,设△P1OA1,△P2A1A2,△P3A2A3,…的面积分别为S1,S2,S3,…依据图形所反映的规律,S2019=_____.
x+4上,设△P1OA1,△P2A1A2,△P3A2A3,…的面积分别为S1,S2,S3,…依据图形所反映的规律,S2019=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
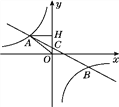
【题目】【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=![]() ,点B的坐标为(m,-2).
,点B的坐标为(m,-2).
(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
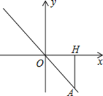
【题目】如图,正比例函数y=kx的图像经过点A,点A在第四象限.过点A做AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为4.5.
(1)求该正比例函数的解析式;
(2)在x轴上是否存在一点P,使△AOP的面积为6?若存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
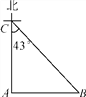
【题目】如图,海面上B,C两岛分别位于A岛的正东和正北方向.一艘船从A岛出发,以18海里/时的速度向正北方向航行2小时到达C岛,此时测得B岛在C岛的南偏东43°.求A,B两岛之间的距离.(结果精确到0.1海里)(参考数据:sin43°=0.68,cos43°=0.73,tan43°=0.93)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com