
【题目】如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过网格点A(0,4)、B(-4,4)、C(-6,2),请在网格图中进行如下操作:
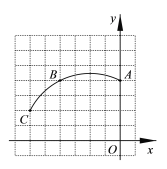
(1)利用网格图确定该圆弧所在圆的圆心D的位置(保留画图痕迹);
(2)连接AD、CD,则⊙D的半径为_ __(结果保留根号),∠ADC的度数为_ __;
(3)若扇形DAC是一个圆锥的侧面展开图,求该圆锥底面半径.(结果保留根号).
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,圆M经过原点O,直线![]() 与x轴、y轴分别相交于A,B两点.
与x轴、y轴分别相交于A,B两点.
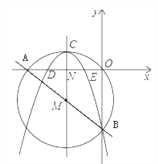
(1)求出A,B两点的坐标;
(2)若有一抛物线的对称轴平行于y轴且经过点M,顶点C在圆M上,开口向下,且经过点B,求此抛物线的函数解析式;
(3)设(2)中的抛物线交![]() 轴于D、E两点,在抛物线上是否存在点P,使得S△PDE=
轴于D、E两点,在抛物线上是否存在点P,使得S△PDE=![]() S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,规定把一个三角形先沿x轴翻折,再向右平移两个单位称为一次变换,如图,已知等边三角形ABC的顶点B、C的坐标分别是,(-1,-1),(-3,-1),把三角形ABC经过连续9次这样的变换得到三角形A’B’C’,则点A的对应点A’的坐标是_____
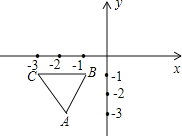
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市举行八年级“生活中的数学知识”竞赛活动,甲、乙两校分别派五名同学参加竞赛,其成绩分别是(单位:分):甲校五名同学:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;乙校五名同学:
;乙校五名同学:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .根据以上数据解答下列问题:
.根据以上数据解答下列问题:
![]() 把表格空格填完整:
把表格空格填完整:
学校 | 平均数(分) | 中位数(分) | 众数(分) |
甲校五位同学 | ________ |
| ________ |
乙校五位同学 |
| ________ |
|
![]() 根据上述数据,请你分析哪所学校同学的竞赛成绩相对较好?
根据上述数据,请你分析哪所学校同学的竞赛成绩相对较好?
查看答案和解析>>
科目:初中数学 来源: 题型:
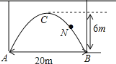
【题目】一拱形隧道的轮廓是抛物线如图,拱高![]() ,跨度
,跨度![]() .
.
![]() 建立适当的直角坐标系,求拱形隧道的抛物线关系式;
建立适当的直角坐标系,求拱形隧道的抛物线关系式;
![]() 拱形隧道下地平面是双向行车道(正中间是一条宽
拱形隧道下地平面是双向行车道(正中间是一条宽![]() 的隔离带),其中的一条行车道能否并排行驶宽
的隔离带),其中的一条行车道能否并排行驶宽![]() ,高
,高![]() 的三辆汽车(汽车间的间隔忽略不计)?请说说你的理由.
的三辆汽车(汽车间的间隔忽略不计)?请说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=2,点E是AB上一点,将正方形沿CE折叠,点B落在正方形内一点B'处,若△AB'D为等腰三角形,则BE的长度为_____.
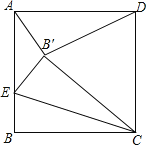
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() ,与
,与![]() 轴交于
轴交于![]() 点,且与
点,且与![]() 轴交点的横坐标分别为
轴交点的横坐标分别为![]() 、
、![]() ,其中
,其中![]() ,
,![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的有( )
.其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是边长为
是边长为![]() 的正方形
的正方形![]() 对角线
对角线![]() 上一动点(
上一动点(![]() 与
与![]() 、
、![]() 不重合),点
不重合),点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
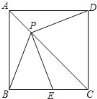
![]() 求证:①
求证:①![]() ;②
;②![]() ;
;
![]() 设
设![]() ,
,![]() 的面积为
的面积为![]() .
.
①求出![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
②当![]() 取何值时,
取何值时,![]() 取得最大值,并求出这个最大值.
取得最大值,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正面分别写着数字1,2,3的三张卡片(注:这三张卡片的形状、大小、质地,颜色等其他方面完全相同,若背面上放在桌面上,这三张卡片看上去无任何差别)洗匀后,背面向上放在桌面上,从中先随机抽取一张卡片,记该卡片上的数字为x,再把剩下的两张卡片洗匀后,背面向上放在桌面上,再从这两张卡片中随机抽取一张卡片,记该卡片上的数字为y.
(1)用列表法或树状图法(树状图也称树形图)中的一种方法,写出(x,y)所有可能出现的结果.
(2)求取出的两张卡片上的数字之和为偶数的概率P.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com