
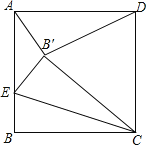
【题目】如图,正方形ABCD中,AB=2,点E是AB上一点,将正方形沿CE折叠,点B落在正方形内一点B'处,若△AB'D为等腰三角形,则BE的长度为_____.
【答案】4﹣2![]() 或
或![]() .
.
【解析】
由四边形ABCD是正方形,得到AB=BC=CD=AD,因为△AB'D为等腰三角形,分三种情况:①AD=B′D;②AB′=B′D③AB′=AD,分别进行讨论即可得出答案.
解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,
①当AD=B′D时,如图1,
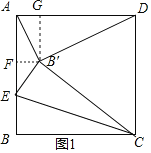
由折叠的性质得,B′C=BC,
∴B′D=B′C=CD,
∴△CDB′是等边三角形,
∴∠B′DC=60°,
∴∠ADB′=30°,
过B′作B′G⊥AD于G,B′F⊥AB于F,
∴AF=B′G=![]() =
=![]() ×2=1,DG=
×2=1,DG=![]() =
=![]() ,
,
∴AG=FB′=2﹣![]() ,
,
∵BE=B′E,EF=1﹣BE,![]()
∴(2﹣![]() )2+(1﹣BE)2=BE2,
)2+(1﹣BE)2=BE2,
∴BE=4﹣2![]() ;
;
②当AB′=B′D时,如图2,

则B′在AD的垂直平分线上,
∴B′在BC的垂直平分线上,
∴BB′=CB′,
由折叠的性质得,B′C=BC,
∴△BB′C是等边三角形,
∴∠BCE=30°,
∴BE=![]() BC=
BC=![]() ,
,
③当AB′=AD时,则AB=AB′,
∵EB=EB′,CB=CB′,
∴点E、C在BB′的垂直平分线上,
∴EC垂直平分BB′,
∴A与E重合,
∴B′与D重合,不符合题意,舍去.
综上所述,BE的长为4﹣2![]() 或
或![]() .
.
故答案为:4﹣2![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() .
.
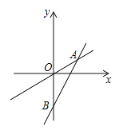
(1)求一次函数的表达式;
(2)求两直线与![]() 轴围成的三角形的面积.
轴围成的三角形的面积.
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 是以
是以![]() 为腰的等腰三角形,若存在,直接写出
为腰的等腰三角形,若存在,直接写出![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你同意下面的说法吗?说明你的理由.
![]() 在掷骰子游戏中,掷得“
在掷骰子游戏中,掷得“![]() ”的概率是
”的概率是![]() 的意思是:每掷
的意思是:每掷![]() 次,一定会有
次,一定会有![]() 次出现“
次出现“![]() ”.
”.
![]() 九年级
九年级![]() 班共有
班共有![]() 名同学.其中男同学
名同学.其中男同学![]() 名,女同学
名,女同学![]() 名.数学老师任意点一名同学回答问题,点到的同学可能是男同学,也可能是女同学,所以点到男同学的概率是
名.数学老师任意点一名同学回答问题,点到的同学可能是男同学,也可能是女同学,所以点到男同学的概率是![]() .
.
![]() 一种福利彩票中奖的概率是
一种福利彩票中奖的概率是![]() ,李大爷买回一张这种福利彩票,李大爷的孙子说:“您不可能中奖,因为中奖的概率太小了!”
,李大爷买回一张这种福利彩票,李大爷的孙子说:“您不可能中奖,因为中奖的概率太小了!”
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过网格点A(0,4)、B(-4,4)、C(-6,2),请在网格图中进行如下操作:
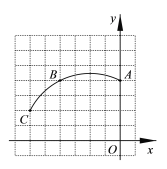
(1)利用网格图确定该圆弧所在圆的圆心D的位置(保留画图痕迹);
(2)连接AD、CD,则⊙D的半径为_ __(结果保留根号),∠ADC的度数为_ __;
(3)若扇形DAC是一个圆锥的侧面展开图,求该圆锥底面半径.(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
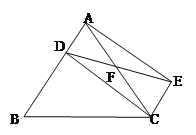
【题目】如图,D是△ABC的边AB上一点,CE∥AB,DE交AC于点F,若FA=FC.
(1)求证:四边形ADCE是平行四边形;
(2)若AE⊥EC,EF=EC=1,求四边形ADCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,其部分图象如图所示.则下列结论:①
之间,其部分图象如图所示.则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() (
(![]() 为实数);⑤点
为实数);⑤点![]() ,
,![]() ,
,![]() 是该抛物线上的点,则
是该抛物线上的点,则![]() ,正确的个数有( )
,正确的个数有( )
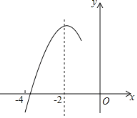
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
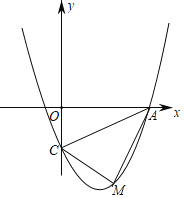
【题目】如图,抛物线经过点A(4,0)、B(﹣2,0)、C(0,﹣4)
(1)求抛物线的解析式;
(2)在抛物线AC段上是否存在点M,使△ACM的面积为3,求出在此时M的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
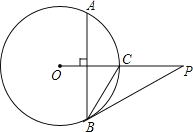
【题目】如图,已知P是⊙O外一点,PO交圆O于点C,OC=CP=2,弦AB⊥OC,劣弧AB的度数为120°,连接PB.
(1)求BC的长;
(2)求证:PB是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com