
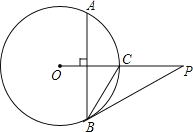
【题目】如图,已知P是⊙O外一点,PO交圆O于点C,OC=CP=2,弦AB⊥OC,劣弧AB的度数为120°,连接PB.
(1)求BC的长;
(2)求证:PB是⊙O的切线.
【答案】(1)2(2)见解析
【解析】解:(1)连接OB,
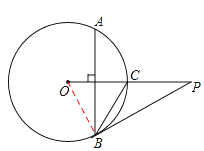
∵弦AB⊥OC,劣弧AB的度数为120°,
∴弧BC与弧AC的度数为:60°。∴∠BOC=60°。
∵OB=OC,∴△OBC是等边三角形。
∵OC =2,∴BC=OC=2。
(2)证明:∵OC=CP,BC=OC,∴BC=CP。
∴∠CBP=∠CPB。
∵△OBC是等边三角形,∴∠OBC=∠OCB=60°。∴∠CBP=30°。
∴∠OBP=∠CBP+∠OBC=90°。∴OB⊥BP。
∵点B在⊙O上,∴PB是⊙O的切线。
(1)连接OB,由弦AB⊥OC,劣弧AB的度数为120°,易证得△OBC是等边三角形,则可求得BC的长。
(2)由OC=CP=2,△OBC是等边三角形,可求得BC=CP,即可得∠P=∠CBP,又由等边三角形的性质,∠OBC=60°,∠CBP=30°,则可证得OB⊥BP,从而证得PB是⊙O的切线。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
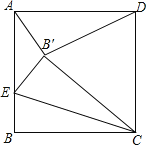
【题目】如图,正方形ABCD中,AB=2,点E是AB上一点,将正方形沿CE折叠,点B落在正方形内一点B'处,若△AB'D为等腰三角形,则BE的长度为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)画出△ABC关于y 轴对称的△A1B1C1,并写出A1、B1、C1的坐标.
(2)将△ABC向右平移6个单位,画出平移后的△A2B2C2;
(3)观察△A1B1C1和△A2B2C2,它们是否关于某直线对称?若是,请在图上画出这条对称轴.

查看答案和解析>>
科目:初中数学 来源: 题型:
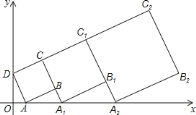
【题目】在平面直角坐标系中,正方形![]() 的位置如图所示,点
的位置如图所示,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .延长
.延长![]() 交
交![]() 轴于点
轴于点![]() ,作正方形
,作正方形![]() ;延长
;延长![]() 交
交![]() 轴于点
轴于点![]() ,作正方形
,作正方形![]() ,按这样的规律进行下去,第
,按这样的规律进行下去,第![]() 个正方形(正方形
个正方形(正方形![]() 看作第
看作第![]() 个)的面积为( )
个)的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正面分别写着数字1,2,3的三张卡片(注:这三张卡片的形状、大小、质地,颜色等其他方面完全相同,若背面上放在桌面上,这三张卡片看上去无任何差别)洗匀后,背面向上放在桌面上,从中先随机抽取一张卡片,记该卡片上的数字为x,再把剩下的两张卡片洗匀后,背面向上放在桌面上,再从这两张卡片中随机抽取一张卡片,记该卡片上的数字为y.
(1)用列表法或树状图法(树状图也称树形图)中的一种方法,写出(x,y)所有可能出现的结果.
(2)求取出的两张卡片上的数字之和为偶数的概率P.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正三角形ABC的边长AB是480毫米.一质点D从点B出发,沿BA方向,以每秒钟10毫米的速度向点A运动.
(1)建立合适的直角坐标系,用运动时间t(秒)表示点D的坐标;
(2)过点D在三角形ABC的内部作一个矩形DEFG,其中EF在BC边上,G在AC边上.在图中找出点D,使矩形DEFG是正方形(要求所表达的方式能体现出找点D的过程);
(3)过点D、B、C作平行四边形,当t为何值时,由点C、B、D、F组成的平行四边形的面积等于三角形ADC的面积,并求此时点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
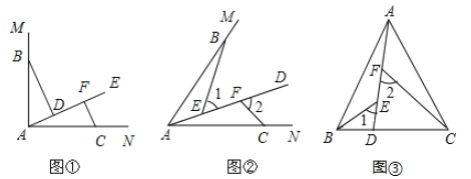
【题目】(1)如图①,![]() ,射线
,射线![]() 在这个角的内部,点
在这个角的内部,点![]() 、
、![]() 分别在
分别在![]() 的边
的边![]() 、
、![]() 上,且
上,且![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .求证:
.求证:![]() ;
;
(2)如图②,点![]() 、
、![]() 分别在
分别在![]() 的边
的边![]() 、
、![]() 上,点
上,点![]() 、
、![]() 都在
都在![]() 内部的射线
内部的射线![]() 上,
上,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的外角.已知
的外角.已知![]() ,且
,且![]() .求证:
.求证:![]() ;
;
(3)如图③,在![]() 中,
中,![]() ,
,![]() .点
.点![]() 在边
在边![]() 上,
上,![]() ,点
,点![]() 、
、![]() 在线段
在线段![]() 上,
上,![]() .若
.若![]() 的面积为15,求
的面积为15,求![]() 与
与![]() 的面积之和.
的面积之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com