
【题目】如图,已知正三角形ABC的边长AB是480毫米.一质点D从点B出发,沿BA方向,以每秒钟10毫米的速度向点A运动.
(1)建立合适的直角坐标系,用运动时间t(秒)表示点D的坐标;
(2)过点D在三角形ABC的内部作一个矩形DEFG,其中EF在BC边上,G在AC边上.在图中找出点D,使矩形DEFG是正方形(要求所表达的方式能体现出找点D的过程);
(3)过点D、B、C作平行四边形,当t为何值时,由点C、B、D、F组成的平行四边形的面积等于三角形ADC的面积,并求此时点F的坐标.

【答案】(1)![]() ;(2) 当点D与点B的距离等于10t=960(2﹣
;(2) 当点D与点B的距离等于10t=960(2﹣![]() )毫米时,矩形是正方形;(3) F(560,80
)毫米时,矩形是正方形;(3) F(560,80![]() ),F′(400,﹣80
),F′(400,﹣80![]() ),F″(﹣400,80
),F″(﹣400,80![]() )
)
【解析】
运用相似三角形及平行四边形的性质求解.
(1)建立如图所示的直角坐标系,作DE⊥x轴于E,
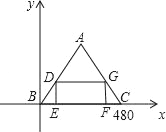
则t秒后,DB=10t
又△ABC是正三角形,故∠B=60°
在Rt△DEB中,DE=DB×sin∠B=10t×![]() =5
=5![]() t,
t,
BE=DB×cos∠B=10t×![]() =5t
=5t
即:D(5t,5![]() );
);
(2)①先画一个正方形,再利用位似图形找出点D,具体作法阅图
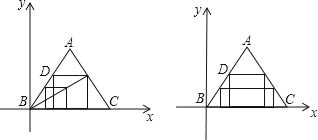
②利用正三角形与矩形是轴对称图形或利用相似三角形的性质求得DG=480﹣10t,DE=5![]() t.然后由480﹣10t=5
t.然后由480﹣10t=5![]() t,
t,
求出t=![]() =96(2﹣
=96(2﹣![]() )(毫米).所以当点D与点B的距离等于10t=960(2﹣
)(毫米).所以当点D与点B的距离等于10t=960(2﹣![]() )毫米时,矩形是正方形.
)毫米时,矩形是正方形.
(3)如图所示:
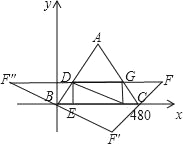
当点F在第一象限时,这个平行四边形是CBDF;
当点F在第二象限时,这个平行四边形是BCDF“;
当点F在第三象限时,这个平行四边形是CDBF'.
但平行四边形BCDF“的面积、平行四边形CDBF'的面积
都与平行四边形CBDF的面积相等(等底等高)
平行四边形CBDF的底BC=480,相应的高是5![]() ,则面积是2400
,则面积是2400![]() ;三角形ADC的底AD=480﹣10t,相应的高是240
;三角形ADC的底AD=480﹣10t,相应的高是240![]()
则面积是120![]() (480﹣10t).
(480﹣10t).
由2400![]() =120
=120![]() (480﹣10t),解得t=16
(480﹣10t),解得t=16
所以当t=16秒时,由点C、B、D、F组成的平
行四边形的面积等于三角形ADC的面积.
∴此时,点F的坐标是F(560,80![]() ),F′(400,﹣80
),F′(400,﹣80![]() ),F″(﹣400,80
),F″(﹣400,80![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,其部分图象如图所示.则下列结论:①
之间,其部分图象如图所示.则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() (
(![]() 为实数);⑤点
为实数);⑤点![]() ,
,![]() ,
,![]() 是该抛物线上的点,则
是该抛物线上的点,则![]() ,正确的个数有( )
,正确的个数有( )
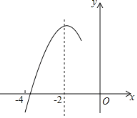
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知![]() ,任取一点
,任取一点![]() ,连
,连![]() ,
,![]() ,
,![]() ,并取它们的中点
,并取它们的中点![]() ,
,![]() ,
,![]() ,得
,得![]() ,则下列说法正确的个数是( )
,则下列说法正确的个数是( )
①![]() 与
与![]() 是位似图形;②
是位似图形;②![]() 与
与![]() 是相似图形;
是相似图形;
③![]() 与
与![]() 的周长比为
的周长比为![]() ;④
;④![]() 与
与![]() 的面积比为
的面积比为![]() .
.
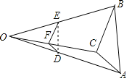
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
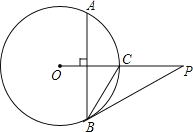
【题目】如图,已知P是⊙O外一点,PO交圆O于点C,OC=CP=2,弦AB⊥OC,劣弧AB的度数为120°,连接PB.
(1)求BC的长;
(2)求证:PB是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
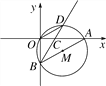
【题目】如图,在直角坐标系中,⊙M经过原点O(0,0),点A(![]() ,0)与点B(0,-
,0)与点B(0,-![]() ),点D在劣弧
),点D在劣弧![]() 上,连结BD交x轴于点C,且∠COD=∠CBO.
上,连结BD交x轴于点C,且∠COD=∠CBO.
(1)求⊙M的半径;
(2)求证:BD平分∠ABO;
(3)在线段BD的延长线上找一点E,使得直线AE恰为⊙M的切线,求此时点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
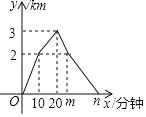
【题目】小明和爸爸周末到湿地公园进行锻炼,两人同时从家出发,匀速骑共享单车到达公园入口,然后一同匀速步行到达驿站,到达驿站后小明的爸爸立即又骑共享单车按照来时骑行速度原路返回,在公园入口处改为步行,并按来时步行速度原路回家,小明到达驿站后逗留了10分钟之后骑车回家,爸爸在锻炼过程中离出发地的路程与出发的时间的函数关系如图.
(1)图中m=_____,n=_____;(直接写出结果)
(2)小明若要在爸爸到家之前赶上,问小明回家骑行速度至少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作:小明准备制作棱长为1cm的正方体纸盒,现选用一些废弃的圆形纸片进行如下设计:
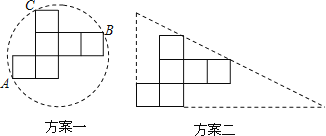
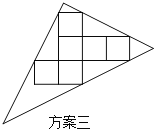
说明:方案一:图形中的圆过点A、B、C;
方案二:直角三角形的两直角边与展开图左下角的正方形边重合,斜边经过两个正方形的顶点.
纸片利用率=![]() ×100%
×100%
发现:(1)方案一中的点A、B恰好为该圆一直径的两个端点.
你认为小明的这个发现是否正确,请说明理由.
(2)小明通过计算,发现方案一中纸片的利用率仅约为38.2%.
请帮忙计算方案二的利用率,并写出求解过程.
探究:
(3)小明感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CECA.
(1)求证:BC=CD;
(2)分别延长AB,DC交于点P,若PB=OB,CD=2![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]() 是
是![]() 内的一点.
内的一点.
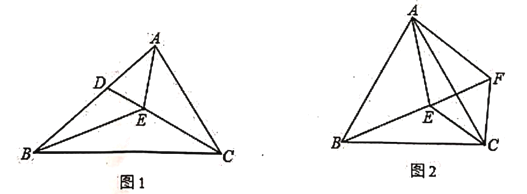
(1)如图,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在线段
在线段![]() 上(点
上(点![]() 不与点
不与点![]() 、
、![]() 重合),且
重合),且![]() ,求证:
,求证:![]() .
.
(2)如图,若![]() 是等边三角形,
是等边三角形,![]() ,
,![]() ,以
,以![]() 为边作等边
为边作等边![]() ,连
,连![]() .当
.当![]() 是等腰三角形时,试求出
是等腰三角形时,试求出![]() 的度数.
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com