
【题目】身高1.65米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形CDEF代表建筑物,兵兵位于建筑物前点B处,风筝挂在建筑物上方的树枝点G处(点G在FE的延长线上).经测量,兵兵与建筑物的距离BC=5米,建筑物底部宽FC=7米,风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上,点A距地面的高度AB=1.4米,风筝线与水平线夹角为37°.
(1)求风筝距地面的高度GF;
(2)在建筑物后面有长5米的梯子MN,梯脚M在距墙3米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根米长的竹竿能否触到挂在树上的风筝?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

【答案】(1)10.4(米) (2)能触到挂在树上的风筝
【解析】
试题分析:(1)过A作AP⊥GF于点P.在Rt△PAG中利用三角函数求得GP的长,从而求得GF的长。
(2)在Rt△MNF中,利用勾股定理求得NF的长度,NF的长加上身高再加上竹竿长,与GF比较大小即可。
解:(1)过A作AP⊥GF于点P,
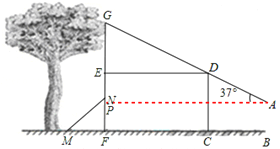
则AP=BF=12,AB=PF=1.4,∠GAP=37°,
在Rt△PAG中,![]() ,
,
∴GP=APtan37°≈12×0.75=9(米)。
∴GF=9+1.4≈10.4(米)。
(2)由题意可知MN=5,MF=3,
∴在直角△MNF中,![]() 。
。
∵10.4﹣5﹣1.65=3.75<4,∴能触到挂在树上的风筝。


科目:初中数学 来源: 题型:
【题目】已知点A(a,0)和B(0,b)满足(a﹣4)2+|b﹣6|=0,分别过点A、B作x轴、y轴的垂线交于点C,如图,点P从原点出发,以每秒2个单位长度的速度沿着O﹣B﹣C﹣A﹣O的路线移动. 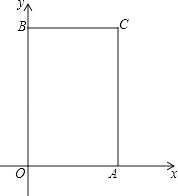
(1)写出A、B、C三点的坐标;
(2)当点P移动了6秒时,描出此时P点的位置,并写出点P的位置;
(3)连结(2)中B、P两点,将线段BP向下平移h个单位(h>0),得到B′P′,若B′P′将四边形OACB的周长分成相等的两部分,求h的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图: 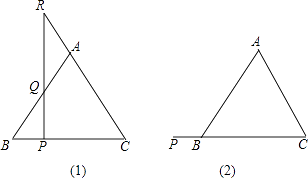
(1)P是等腰三角形ABC底边BC上的一个动点,过点P作BC的垂线,交AB于点Q,交CA的延长线于点R.请观察AR与AQ,它们有何关系?并证明你的猜想.
(2)如果点P沿着底边BC所在的直线,按由C向B的方向运动到CB的延长线上时,(1)中所得的结论还成立吗?请你在图(2)中完成图形,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据民政部网站消息截至2018年底,我国60岁以上老年人口巳经达到2.56亿人。其中2.56 亿用科学记数法表示为( )
A. 2.56×107 B. 2.56×108 C. 2.56×l09 D. 2.56×l010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升![]() cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com