练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】因式分解：

    (1)3x4－48；

    (2)(c2－a2－b2)2－4a2b2.

    【答案】(1) 3(x2＋4)(x＋2)(x－2)；(2) (c＋a－b)(c－a＋b)(c＋a＋b)(c－a－b)．

    【解析】

    (1)应先提取公因式3，再对余下的多项式利用平方差公式继续分解．

    (2) 直接利用平方差公式以及完全平方公式分解因式得出答案．

    (1)原式＝3(x4－16)＝3(x2＋4)(x2－4)＝3(x2＋4)(x＋2)(x－2)；

    (2)原式＝(c2－a2－b2＋2ab)(c2－a2－b2－2ab)＝[c2－(a－b)2][c2－(a＋b)2]

    ＝(c＋a－b)(c－a＋b)(c＋a＋b)(c－a－b)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】甲乙丙丁四支足球队在全国甲级联赛中进球数分别为：9，9，x ， 7，若这组数据的众数与平均数恰好相等，则这组数据的中位数是（ ）
    A.10
    B.9
    C.8
    D.7

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明、小亮、小刚、小颖一起研究一道数学题，如图，已知EF⊥AB，CD⊥AB， 小明说：“如果还知道∠CDG=∠BFE，则能得到∠AGD=∠ACB．”
    小亮说：“把小明的已知和结论倒过来，即由∠AGD=∠ACB，
    可得到∠CDG=∠BFE．”
    小刚说：“∠AGD一定大于∠BFE．”
    小颖说：“如果连接GF，则GF一定平行于AB．”
    他们四人中，有个人的说法是正确的．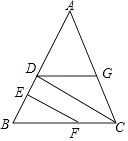

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知 =3，3a+b﹣1的平方根是±4，c是 的整数部分，求a+2b+c的算术平方根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线的顶点坐标是（-1，-2），且经过点（0，1）
    （1）求这个二次函数的解析式；
    （2）写出该抛物线经过怎样的平移后顶点为原点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列结论中不正确的是（　 　）

    A. 平方为9的数是+3或﹣3 B. 立方为27的数是3或﹣3

    C. 绝对值为3的数是3或﹣3 D. 倒数等于原数的数是1或﹣1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，△ABC是边长为4cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，它们的速度都是1cm/s，当点P到达点B时，P、Q两点停止运动，设点P的运动时间t（s），解答下列各问题：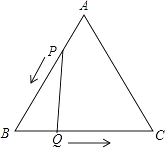
    （1）求△ABC的面积；
    （2）当t为何值是，△PBQ是直角三角形？
    （3）探究：是否存在某一时刻t，使四边形APQC的面积是△ABC面积的八分之五？如果存在，求出t的值；不存在请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

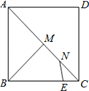
    【题目】如图，正方形ABCD的边长为5，点E在边BC上且CE=2，长为的线段MN在AC上运动，当四边形BMNE的周长最小时，则tan∠MBC的值是(　　)

    A. B. C. D. 1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】身高1.65米的兵兵在建筑物前放风筝，风筝不小心挂在了树上．在如图所示的平面图形中，矩形CDEF代表建筑物，兵兵位于建筑物前点B处，风筝挂在建筑物上方的树枝点G处（点G在FE的延长线上）．经测量，兵兵与建筑物的距离BC=5米，建筑物底部宽FC=7米，风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上，点A距地面的高度AB=1.4米，风筝线与水平线夹角为37°．

    （1）求风筝距地面的高度GF；

    （2）在建筑物后面有长5米的梯子MN，梯脚M在距墙3米处固定摆放，通过计算说明：若兵兵充分利用梯子和一根米长的竹竿能否触到挂在树上的风筝？

    （参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

    查看答案和解析>>

    同步练习册答案