
����Ŀ��С����С����С�ա�Сӱһ���о�һ����ѧ�⣬��ͼ����֪EF��AB��CD��AB�� С��˵���������֪����CDG=��BFE�����ܵõ���AGD=��ACB����
С��˵������С������֪�ͽ��۵����������ɡ�AGD=��ACB��
�ɵõ���CDG=��BFE����
С��˵������AGDһ�����ڡ�BFE����
Сӱ˵�����������GF����GFһ��ƽ����AB����
���������У������˵�˵������ȷ�ģ�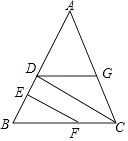
���𰸡���
���������⣺��EF��AB��CD��AB�� ��CD��EF��
����CDG=��BFE��
�ߡ�BCD=��BFE��
���BCD=��CDG��
��DG��BC��
���AGD=��ACB��
��С����˵����ȷ��
����AGD=��ACB��
��DG��BC��
���BCD=��CDG����BCD=��BFE��
���CDG=��BFE��
��С����˵����ȷ��
��DG��һ��ƽ����BC��
���AGD��һ�����ڡ�BFE��
��С�յ�˵������
�������GF����GF��һ��ƽ����AB��
��Сӱ��˵������
����֪����ȷ��˵����������
���Դ��ǣ�����
�����㾫����������Ĺؼ���������ƽ���ߵ��ж������ʵ����֪ʶ�������ɽǵ���Ȼ���������ϵ�����������õ�����ֱ��ƽ�У�λ�ù�ϵ������ƽ���ߵ��ж�����ƽ���ߣ�λ�ù�ϵ���õ��йؽ���Ȼ���������ϵ���Ľ�����ƽ���ߵ����ʣ�


 С��ſ�ʱ��ҵϵ�д�
С��ſ�ʱ��ҵϵ�д� һ������ϵ�д�
һ������ϵ�д� �Ƹ�С״Ԫ���ֳ������ϵ�д�
�Ƹ�С״Ԫ���ֳ������ϵ�д� �¸��̵�ѧϵ�д�
�¸��̵�ѧϵ�д� ����ͬѧһ����ʦȫ�źþ�ϵ�д�
����ͬѧһ����ʦȫ�źþ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�ұ��ݵĵ��ݵ����������Ϊ500 kg������18λ���ؾ�Ϊ57 kg�Ĺ˿�������ܵ�����¥����ô������Ҫ�ּ��β���ȫ����¥��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��BC��OA����B=��A=100�㣬�Իش��������⣺
��1����ͼ1��ʾ����֤��OB��AC�� 
��2����ͼ2������E��F��BC�ϣ��������FOC=��AOC������OEƽ�֡�BOF�������EOC�Ķ����� 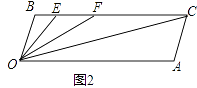
��3���ڣ�2���������£���ƽ���ƶ�AC����ͼ3�����OCB����OFB��ֵ�� �� 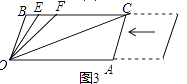
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y��x2��4x��5��x��ֱ���A��B��A��B����ߣ�����y�ύ�ڵ�C��ֱ��AP��y�������ύ�ڵ�M�����������ڵ�P��ֱ��AQ��y�Ḻ���ύ�ڵ�N�����������ڵ�Q����OM��ON����P��Q��ֱ��l
(1) ̽������룺
�� ȡ��M(0��1)��ֱ��д��ֱ��l�Ľ���ʽ
ȡ��M(0��2)��ֱ��д��ֱ��l�Ľ���ʽ
�� ���룺
���Dz���ֱ��l�Ľ���ʽy��kx��b�У�k��Ϊ��ֵ����ֵkΪ__________����ȡM��������Ϊn����֤��IJ���
(2) ��ͼ2������BP��BQ������ABP��������ڡ�ABQ�������3���������ֱ��l�Ľ���ʽ
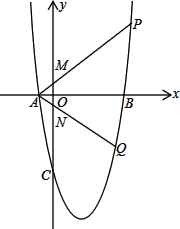
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�һ���ϴ�ԭ��O�����������ϡ����ҡ����¡����ҵķ������β����ƶ���ÿ���ƶ�1����λ��������·����ͼ��ʾ��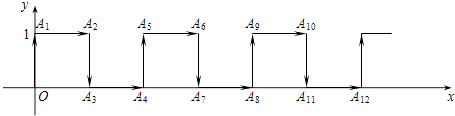
��1����д���и�������꣺A4 �� A8��
��2��д����A4n�����꣨nΪ����������
��3�����ϴӵ�A2014����A2017���ƶ����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������龳����ͼ1��AB��CD����PAB=130�㣬��PCD=120�㣬���APC�Ķ����� С����˼·�ǣ���P��PE��AB��ͨ��ƽ�������������APC��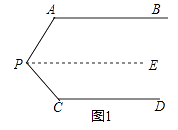
��1����С����˼·������á�APC�Ķ���Ϊ�ȣ�
��2������Ǩ�ƣ���ͼ2��AB��CD����P������OM���˶����ǡ�PAB=������PCD=�£�����P��B��D����֮���˶�ʱ���ʡ�APC�������֮���к�������ϵ����˵�����ɣ� 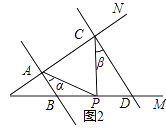
��3���ڣ�2���������£������P��B��D��������˶�ʱ����P���O��B��D���㲻�غϣ�����ֱ��д����APC�������֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��a��0����B��0��b�����㣨a��4��2+|b��6|=0���ֱ����A��B��x�ᡢy��Ĵ��߽��ڵ�C����ͼ����P��ԭ���������ÿ��2����λ���ȵ��ٶ�����O��B��C��A��O��·���ƶ��� 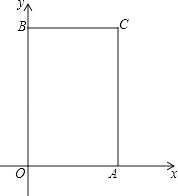
��1��д��A��B��C��������ꣻ
��2������P�ƶ���6��ʱ�������ʱP���λ�ã���д����P��λ�ã�
��3�����ᣨ2����B��P���㣬���߶�BP����ƽ��h����λ��h��0�����õ�B��P�䣬��B��P�佫�ı���OACB���ܳ��ֳ���ȵ������֣���h��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com