
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数. 小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.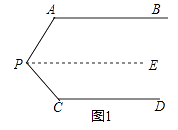
(1)按小明的思路,易求得∠APC的度数为度;
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由; 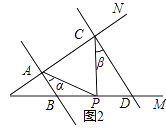
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.
【答案】
(1)110
(2)解:∠APC=∠α+∠β,
理由:如图2,过P作PE∥AB交AC于E,
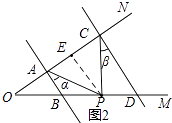
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠APE+∠CPE=∠α+∠β
(3)解:如图所示,当P在BD延长线上时,
∠CPA=∠α﹣∠β;
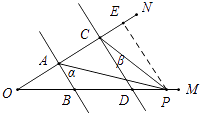
如图所示,当P在DB延长线上时,
∠CPA=∠β﹣∠α.

【解析】(1)解:过点P作PE∥AB, ∵AB∥CD,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°,
∴∠APC=∠APE+∠CPE=110°.
【考点精析】根据题目的已知条件,利用平行线的性质的相关知识可以得到问题的答案,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.


 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源: 题型:
【题目】某商场第一季度的利润是82.75万元,其中一月份的利润是25万元,若利润平均每月的增长率为x , 则依题意列方程为( )
A.25(1+x)2=82.75
B.25+50x=82.75
C.25+25(1+x)2=82.75
D.25[1+(1+x)+(1+x)2]=82.75
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1).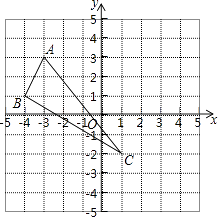
(1)请画出△ABC沿x轴向右平移3个单位长度,再沿y轴向上平移2个单位长度后的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法).
(2)直接写出A′、B′、C′三点的坐标:
A′( , ); B′( , );
C′( , ).
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小亮、小刚、小颖一起研究一道数学题,如图,已知EF⊥AB,CD⊥AB, 小明说:“如果还知道∠CDG=∠BFE,则能得到∠AGD=∠ACB.”
小亮说:“把小明的已知和结论倒过来,即由∠AGD=∠ACB,
可得到∠CDG=∠BFE.”
小刚说:“∠AGD一定大于∠BFE.”
小颖说:“如果连接GF,则GF一定平行于AB.”
他们四人中,有个人的说法是正确的.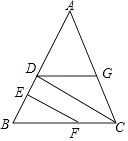
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠OAB=45°,点A的坐标是(4,0),AB= ![]() ,连结OB.
,连结OB.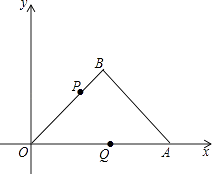
(1)直接写出点B的坐标.
(2)动点P从点O出发,沿折线O﹣B﹣A方向向终点A匀速运动,另一动点Q从点O出发,沿OA方向匀速运动,若点P的运动速度为 ![]() 个单位/秒,点Q的运动速度是1个单位/秒,P、Q两点同时出发,设运动时间为t秒,请求出使△OPQ的面积等于1.5时t的值.
个单位/秒,点Q的运动速度是1个单位/秒,P、Q两点同时出发,设运动时间为t秒,请求出使△OPQ的面积等于1.5时t的值.
(3)动点P仍按(2)中的方向和速度运动,但Q点从A点向O点运动,速度为1个单位/秒,P、Q与△OAB中的任意一个顶点形成直角三角形时,求此时t(t≠0)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是边长为4cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间t(s),解答下列各问题: 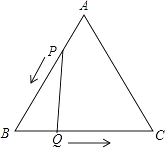
(1)求△ABC的面积;
(2)当t为何值是,△PBQ是直角三角形?
(3)探究:是否存在某一时刻t,使四边形APQC的面积是△ABC面积的八分之五?如果存在,求出t的值;不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A成的距离y(千米)与甲车行驶的时间t(时)之间的关系如图所示,观察图象回答下列问题: 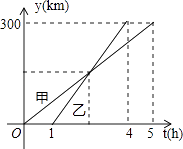
(1)A,B两城相距千米;
(2)若两车同时出发,乙车将比甲车早到小时;
(3)乙车的速度为千米/时;乙车出发后小时两车相遇;
(4)直接写出,当乙车出发几小时,甲、乙两车相距40千米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com